[Chapter 7~13] Problems #2 (2)

[Problem 1.0]

함수 $f(x)=x-\tan x$가 무수히 많은 양의 실근 $x_1,x_2,\cdots$을 가짐을 보이시오. 또한, $n\to \mathrm{\infty }$일 때 $x_n-g(n)\to 0$인 간단한 함수 $g(n)$을 하나 찾으시오.

증명 ▶

(Proof)

$f(n\pi )>0,{\displaystyle \underset{x\to (n+1/2){\pi }^{+}}{lim}f(x)\to -\mathrm{\infty }}$이므로 사잇값 정리에 의하여 $n\pi <x_n<(n+1/2)\pi$인 것을 알 수 있다.

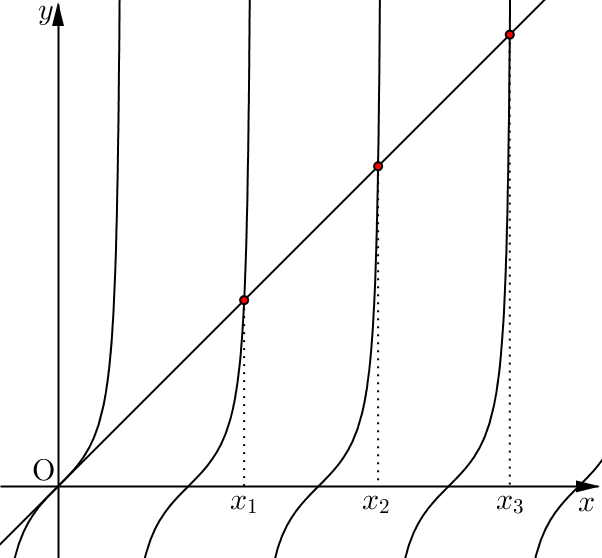
이때 $x_n=\tan x_n$이고 ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}{x}_n=\mathrm{\infty }}$이므로 ${\displaystyle \underset{n\to \mathrm{\infty }}{lim}\tan x_n=\mathrm{\infty }}$이다. 따라서 $g(n)=(n+1/2)\pi$라 두면 $n\to \mathrm{\infty }$일 때 $x_n-g(n)\to 0$이다. 

[Cf] $n\to \mathrm{\infty }$일 때, $$\begin{array}{rl}\tan (x_n-g(n))& =\tan (x_n-(n+1/2)\pi )\\ & =\cot (x_n)\\ & =1/x_n\to 0\end{array}$$이고 $-\pi /2<x_n-g(n)<0$이므로 $x_n-g(n)\to 0$이다.

증명 ▶

[Example 1.1]

함수 $f(x)$는 $\mathbb{R}$에서 연속, $f(x)>0$이고 ${\displaystyle \underset{n\to \pm \mathrm{\infty }}{lim}f(x)=0}$을 만족시킨다. 함수 $f(x)$가 $\mathbb{R}$에서 최솟값은 가지지 않고, 최댓값을 가진다는 것을 보여라.

증명 ▶

(Proof)

${\displaystyle \underset{n\to \pm \mathrm{\infty }}{lim}f(x)=0}$이므로 임의의 양수 $ϵ$에 대하여 양수 $M_1$이 존재하여 $|x|>M_1$일 때마다 $f(x)<ϵ$을 만족시킨다. 또, 닫힌구간 $[-M_1,M_1]$에서 함수 $f(x)$의 최솟값을 $m$이라 하면 양수 $M_2$가 존재하여 $|x|>M_2$일 때마다 $f(x)<m/2$를 만족시킨다. 따라서 $|x|>M:=max\{M_1,M_2\}$일 때마다 $f(x)<min\{ϵ,m/2\}$를 만족시킨다. 즉, $inf\{f(x):x\in \mathbb{R}\}=0$이다. 이때 $f(x)>0$이므로 함수 $f(x)$는 최솟값을 갖지 않는다. 

비슷한 방법으로, 어떤 양수 $K$에 대하여 닫힌구간 $[-K,K]$에서의 최댓값을 $M^{\ast }$이라 하면 양수 $K^{\prime }\ge K$가 존재하여 $|x|>K^{\prime }$일 때마다 $f(x)<M^{\ast }/2$을 만족시킨다. 따라서 닫힌구간 $[-K^{\prime },K^{\prime }]$에서의 함수 $f(x)$의 최댓값이 $\mathbb{R}$에서의 최댓값이다. 

[Cf] $\mathbb{R}$의 유계이고 닫힌 집합 $D$에서(즉, 콤팩트집합에서) 연속인 함수는 항상 최댓값과 최솟값을 갖는다.

증명 ▶

[Example 1.2]

함수 $f(x)$가 구간 $I$와 $J$에서 균등연속(uniformly continuous)이고 $I\cap J\ne \varnothing$일 때, $f(x)$는 구간 $I\cup J$에서 균등연속임을 보여라. 

증명 ▶

(Proof)

$x,y\in I\cup J$라고 하자. 임의의 양수 $ϵ$에 대하여

(1) $x,y\in I$인 경우 (또는 $x,y\in J$인 경우)
함수 $f(x)$는 구간 $I$와 $J$에서 각각 균등연속이므로 $\delta >0$이 존재하여 $|x-y|<\delta$일 때마다 $|f(x)-f(y)|<ϵ/2<ϵ$을 만족시킨다.

(2) $x\in I,y\in J$인 경우 (또는 $x\in J,y\in I$인 경우) 
(1)의 $\delta >0$에 대하여 $|x-y|<\delta$라 하면 $z\in I\cap J$가 존재하여 $|x-z|<\delta$이고 $|z-y|<\delta$이므로 $$|f(x)-f(z)|<ϵ/2,|f(z)-f(y)|<ϵ/2$$를 만족시킨다. 따라서 $|x-y|<\delta$라 하면 $$\begin{array}{rl}|f(x)-f(y)|& \le |f(x)-f(z)|+|f(z)-f(y)|\\ & <ϵ/2+ϵ/2=ϵ\end{array}$$이다.

(1), (2)로부터 임의의 $x,y\in I\cup J$와 $ϵ>0$에 대하여 양수 $\delta$가 존재하여 $|x-y|<\delta$일 때마다 $|f(x)-f(y)|<ϵ$을 만족시키므로 함수 $f(x)$는 구간 $I\cup J$에서 균등연속이다.

증명 ▶

[Example 1.3]

(1) 함수 $f(x)$가 구간 $I$에서 균등연속이고, 수열 $\{a_n\}$이 $I$ 위에서의 코시 수열이면, $\{f(a_n)\}$도 코시 수열임을 보여라.
(2) (1)을 이용하여 함수 $f(x)$가 $I=(a,b)$에서 균등연속이면 $I$에서 유계임을 보여라.

증명 ▶

(Proof)

(1) 함수 $f(x)$가 $I$에서 균등연속이므로 임의의 양수 $ϵ$에 대하여 $\delta >0$이 존재하여 $|x-y|<\delta$일 때마다 $|f(x)-f(y)|<ϵ$을 만족시킨다. 한편 수열 $\{a_n\}$이 코시 수열이므로 자연수 $n_0$이 존재하여 $m,n>n_0$일 때마다 $|a_m-a_n|<\delta$를 만족시킨다. 따라서 $|f(a_m)-f(a_n)|<ϵ$이므로 수열 $\{f(a_n)\}$은 코시 수열이다.

(2) $f(x)$가 위로 유계가 아니라고 가정하자. 그러면 함수 $f(x)$가 $I$에서 연속이므로 ${\displaystyle \underset{x\to a+}{lim}f(x)=\mathrm{\infty }}$ 또는 ${\displaystyle \underset{x\to b-}{lim}f(x)=\mathrm{\infty }}$이다. ${\displaystyle \underset{x\to a+}{lim}f(x)=\mathrm{\infty }}$이라 가정하자. 이때 수열 $$\{x_n\}:x_n=a+1/n$$은 $I$ 위에서의 코시 수열이지만 수열 $\{f(x_n)\}$은 명백히 코시 수열이 아니다. 이는 (1)과 모순이다. 따라서 $f(x)$는 위로 유계이다. 비슷한 방법으로 $f(x)$가 아래로 유계임도 보일 수 있다.

증명 ▶

[Example 1.4]

Strengthened version of [Example 1.3]: 함수 $f:K\to \mathbb{R}$이 연속이고 $K$가 콤팩트집합이면 $f[K]$도 콤팩트집합임을 보여라.

증명 ▶

(Proof)

$\mathbb{R}$ 위의 보통 위상 $\mathcal{U}$에 대하여 $\mathcal{G}=\{G\mid G\in \mathcal{U}\}$를 $f[K]$의 한 열린 덮개라고 하자. 함수 $f$가 연속이므로 $f^{-1}[\mathcal{G}]=\{f^{-1}[G]\mid G\in \mathcal{U}\}$는 $K$의 한 열린 덮개이다. $K$는 콤팩트집합이므로 $f^{-1}[G]$는 유한인 열린부분덮개 ${\mathcal{G}}^{\ast }=\{f^{-1}[G_1],f^{-1}[G_2],\cdots ,f^{-1}[G_m]\}$를 갖는다. 이때 $$\begin{array}{rl}f[K]& \subset f\left({\displaystyle \bigcup _{k=1}^m{f}^{-1}[G_k]}\right)\\ & ={\displaystyle \bigcup _{k=1}^{m}f(f^{-1}[G_k])\subset {\displaystyle \bigcup _{k=1}^m{G}_k}}\end{array}$$이므로 $\{G_1,G_2,\cdots ,G_m\}$은 $\mathcal{G}$의 유한인 열린부분덮개이다. 즉, $f[K]$의 임의의 열린덮개는 유한인 부분덮개를 가지므로 $f[K]$는 콤팩트집합이다. 

[Cf] 이 명제의 자명한 결과로 <최대, 최소의 정리>를 얻는다. 

'닫힌구간 $[a,b]$에서 연속인 함수 $f$는 그 구간에서 항상 최댓값과 최솟값을 갖는다.'

증명 ▶

 

Reference: <Introduction to Analysis> Arthur Mattuck, 1999.