[Problem 0.0]
모든 자연수 \(n\)에 대하여 \(a_n\geq 0, \; b_n \geq 0\)이고 \(\sum a_n^{\;2}\,\)과 \(\sum b_n^{\;2}\,\)이 수렴하면 \(\sum a_nb_n\)도 수렴함을 증명하시오.
# Solution ▶
(Proof)
\(a_n\geq 0\)이고 \(b_n\geq 0\)이므로 \(a_nb_n\leq (a_n^{\;2}+b_n^{\;2})/2\)이다. 이때 문제의 조건으로부터 \(\sum(a_n^{\;2}+b_n^{\;2})/2\,\)이 수렴하므로 단조 수렴 정리(또는 유계 수렴 정리)에 의하여 \(\sum a_nb_n\)도 수렴한다.
[cf] \(a_n, \, b_n\geq 0\)이므로 \(\displaystyle \sum_{k=1}^{n} a_nb_n\)은 증가하는 수열이다. 또한, 이 부분합 수열은 \(\sum(a_n^{\;2}+b_n^{\;2})/2\,\)의 값에 의하여 위로 유계이다. 따라서 단조 수렴 정리에 의하여 \(\sum a_nb_n\)은 수렴한다.
# ◀ 닫기
[Problem 0.1]
다음 급수가 수렴하는지 판정하시오: \(\displaystyle \sum_{n=1}^{\infty} (-1)^n (\sqrt[n]{n}-1)\)
# Solution ▶
(Proof)
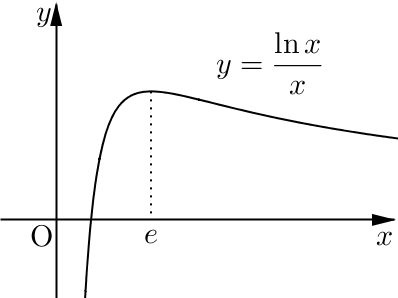
\(\displaystyle a_n=\frac{\ln n}{n}\,\)이라 하자. 함수 \(\displaystyle y=\frac{\ln x}{x}\)는 \(x>e\)일 때 감소하므로(그림 참고) \(n\geq 3\)일 때 수열 \(\{a_n\}\)은 감소한다. 따라서 \(n\geq 3\)일 때 수열 \(\{\sqrt[n]{n}-1\}\)은 감소한다. 또한 \(\displaystyle \lim_{n\rightarrow \infty}\{\sqrt[n]{n}-1\}=0\,\)이다. 따라서 교대급수의 수렴 판정법에 의하여 주어진 급수는 수렴한다.
# ◀ 닫기
[Problem 0.2]
임의의 정수 \(k\)에 대하여 구간 \(\displaystyle \left[2k\pi+\frac{\pi}{4}, 2k\pi+\frac{3\pi}{4}\right]\)에 정수가 적어도 하나 존재함을 이용하여 급수 \(\displaystyle \sum \frac{\sin n}{n}\)이 절대수렴하지 않음을 보여라.
# Solution ▶
(Proof)
주어진 구간 \(I_k:=\displaystyle \left[2k\pi+\frac{\pi}{4}, 2k\pi+\frac{3\pi}{4}\right]\)의 길이가 \(\pi/2>1\)이므로 주어진 구간 안에는 정수가 적어도 하나 존재한다. 구간 \(I_k\)에서 \(\sin x\geq 1/\sqrt{2}\)이므로 \[\begin{align}\sum\left|\frac{\sin n}{n}\right| & \geq \sum_{n\in I_k}\frac{\sin n}{n} \\[.3em] & \geq \sum \frac{1/\sqrt{2}}{2n\pi+3\pi/4} \rightarrow \infty \end{align}\]이다. 따라서 주어진 급수는 절대수렴하지 않는다.
[Cf] 모든 자연수 \(n\)에 대하여 \[\begin{align} \int_{n\pi}^{(n+1)\pi}\left|\frac{\sin x}{x}\right|dx &\geq \frac{1}{(n+1)\pi}\int_{n\pi}^{(n+1)\pi}|\sin x|\,dx \\[.3em]&=\frac{2}{(n+1)\pi} \end{align}\]이므로 \[\begin{align}\sum_{k=1}^{n}\int_{k\pi}^{(k+1)\pi}\left|\frac{\sin x}{x}\right|dx &=\int_{\pi}^{(n+1)\pi}\left|\frac{\sin x}{x}\right|dx \\[.3em]&\geq \sum_{k=1}^{n} \frac{2}{(k+1)\pi} \rightarrow \infty \;\; \text{as} \;\; n\rightarrow \infty\end{align}\]이다. 따라서 적분 판정법(integral test)에 의하여 주어진 급수는 발산한다.
# ◀ 닫기
[Problem 0.3]
급수 \(\sum (\sin n)x^n\,\)의 수렴 반경을 구하시오.
# Solution ▶
(Proof)
[Problem 0.2]에서 구간 \(I_k:=\displaystyle \left[2k\pi+\frac{\pi}{4}, 2k\pi+\frac{3\pi}{4}\right]\)에는 정수가 적어도 하나 존재한다. 따라서 \(\displaystyle \overline{\lim_{n\rightarrow \infty}}\sqrt[n]{|\sin n|}\geq \lim_{n\rightarrow \infty}(1/\sqrt{2})^{1/n}=1\)이다. 또한 \(|\sin n|\leq 1\)이므로 \(\displaystyle \overline {\lim_{n\rightarrow \infty}}\sqrt[n]{|\sin n|}=1\)이다. 근 판정법(root test)에 의하여 주어진 거듭제곱급수의 수렴 반경은 \(1\)이다.
# ◀ 닫기
[Problem 0.4]
함수 \(f(x)=\displaystyle \int_0^\pi \frac{\cos xt}{1+t}dt\,\)가 \(x=0\)에서 연속임을 증명하시오.
# Solution ▶
(Proof)
\[\begin{align} |f(x)-f(0)|&=\int_0^\pi \frac{1-\cos xt}{1+t}dt \\[.3em] &\leq \int_0^\pi(1-\cos xt)dt \\[.3em] &\leq \int_0^\pi \left(\frac{x^2t^2}{2}\right)dt \\[.3em] &=\frac{\pi^3}{6}x^2 \rightarrow 0 \;\; \text{as} \;\; x\rightarrow 0\end{align}\]이므로 \(\displaystyle \lim_{x\rightarrow 0}f(x)=f(0)\)을 얻는다.
# ◀ 닫기
Reference: <Introduction to Analysis> Arthur Mattuck, 1999.
'[Undergraduates] > 해석학' 카테고리의 다른 글
| [Chapter 7~13] Problems #2 (2) (0) | 2021.03.15 |
|---|---|
| [Chapter 1~6] Problems #1 (0) | 2021.03.07 |
| 무한(infinite)이란 무엇인가? (0) | 2021.02.26 |