연결집합과 비연결집합
위상수학에서의 공간에 대한 논의는 모두 열린 집합으로부터 비롯된다. 연결성도 마찬가지인데, 크게 보면 연결집합이란 두 개의 서로소인 열린 집합으로 떼어낼 수 없는 집합을 의미한다. \(\Bbb R\)에서 예를 들어 집합 \(A=[-1, \,1]\)은 연결집합이지만 \(A\cap \Bbb Q\)는 연결집합이 아니다. \(A\cap \Bbb Q\)는 두 열린구간 \((-2, \, 1/\sqrt{2}), \; (1/\sqrt{2}, \,2)\)로 분리할 수 있기 때문이다.
연결성을 논의하기 위해 맨 처음 두 집합의 '분리'에 대해 얘기해야 한다. 위의 예시로부터 확장하여 분리된 두 개의 열린 집합에 의하여 나눌 수 있는 집합을 비연결집합이라고 하기 때문이다.
[Definition 1.0]
위상공간 \(X\)의 두 부분집합 \(A, \, B\)가 \[A\cap \bar B=\varnothing, \quad \bar A\cap B=\varnothing\]을 만족시키면 두 집합 \(A, \, B\)가 서로 분리된(seperated) 집합이라고 한다.
분리된 집합과 서로소인 집합은 의미가 다르다. 분리된 집합이 더 강한 의미를 갖는다.
[Example 1.1]
\(\Bbb R\)의 세 부분집합 \(A=(0, 1)\), \(B=(1, 2)\), \(C=[2, 3)\)에 대하여 \(\bar A=[0, 1]\), \(\bar B=[1, 2]\)이므로 \(A\cap \bar B=\bar A\cap B=\varnothing\)이다. 따라서 두 집합 \(A\)와 \(B\)는 서로소이면서 서로 분리된 집합이다.
반면, \(B\cap C=\varnothing\)이고 \(\bar B\cap C\neq \varnothing\)이므로 \(B\)와 \(C\)는 서로소이나 서로 분리된 집합은 아니다.
[Example 1.2]
\(\Bbb R^2\)의 두 부분집합 \(A\), \(B\)을 \[\begin{align}&A=\{(0, y): 1/2\leq y\leq 1\}\\[.5em] &B=\{(x, y): y=\sin(1/x), \; 0<x\leq 1\}\end{align}\]라 하면 이 둘은 서로소이다. 그러나 집합 \(B\)의 집적점들은 모두 집합 \(A\)에 속하므로 (\(y\)축의 근방에서 함수 \(y=\sin(1/x)\)의 그래프가 딱 붙어서 그려지는 것을 볼 수 있다.) 따라서 두 집합 \(A\)와 \(B\)는 서로 분리된 집합이 아니다.
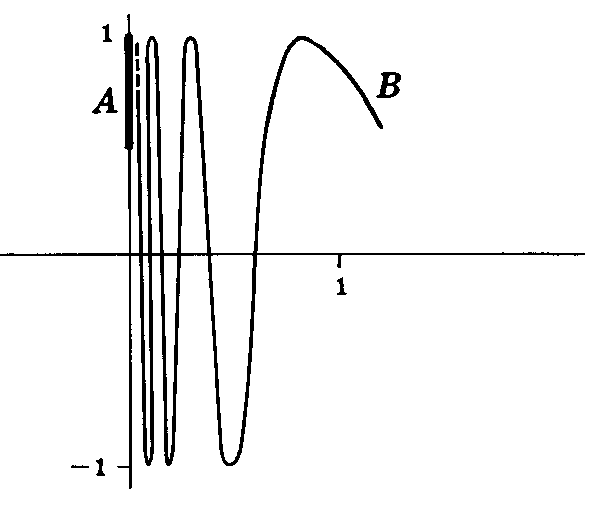
이를 이용하여 연결집합의 정의를 할 수 있다. 참고할 것은, 연결집합은 '비연결'이라는 것을 이용하여 정의된다는 것에 초점을 맞추면 좋다. 즉, '연결'이 무엇이라 정의하는 것이 아니라 '비연결'이 무엇인지 정의하고 그것이 아닌 것을 '연결'이라고 하는 것이다.
[Definition 1.3]
위상공간 \(X\)의 부분집합 \(A\)이 다음 조건을 만족시키면 \(A\)를 비연결인(disconnected) 집합이라고 하고, \(A\)가 비연결인 집합이 아닌 경우, \(A\)를 연결된(connected) 집합이라고 하자.
[Condition] \(A\cap G\neq \varnothing\), \(A\cap H\neq \varnothing\), \((A\cap G)\cap (A\cap H)=\varnothing\), \((A\cap G)\cup (A\cap H)=A\)인 두 열린 집합 \(G\), \(H\)가 존재한다.
이때 \(G\cup H\)를 집합 \(A\)의 비연결(disconnection)이라고 한다.
즉, 비연결집합이란 서로소인 두 열린 집합(부분공간의 측면에서)을 이용하여 분리할 수 있는 집합을 의미한다. 그러나 두 열린 집합이 전체 공간에서 서로소일 필요는 없다.
[Example 1.4]
집합 \(X=\{a, b, c, d, e\}\) 위의 위상 \(\mathcal T\)가 \[\mathcal T=\{X, \, \varnothing, \, \{a, b, c\}, \, \{c, d, e\},\, \{e\}\}\]로 주어졌다고 하자. \(A=\{a, d, e\}\)는 비연결집합이다. 두 열린 집합 \(G=\{a, b, c\}\)와 \(H=\{c, d, e\}\)에 대하여 \(A\cap G=\{a\}\), \(A\cap H=\{d, e\}\)이고 이 둘은 서로소이면서 합집합은 \(A\)가 된다. 이때 \(G\cap H\neq \varnothing\)이다.
이때 비연결집합은 (부분공간에서) 서로소인 열린 집합의 합집합으로 나타나는 집합이므로, 닫힌 집합의 성질에 의하여 두 열린 집합은 (부분공간에서) 분리된 집합이 된다.
[Theorem 1.5]
어떤 집합이 비연결집합일 필요충분조건은 그 집합이 서로 분리된 공집합이 아닌 두 집합의 합집합인 것이다.
# 증명 ▶
(Proof)
(\(\Rightarrow\)) 위상공간 \(X\)의 부분집합 \(A\)가 비연결집합이라고 하자. 그러면 두 열린 집합 \(G\), \(H\)이 존재하여 집합 \(A\)의 비연결을 이룬다. 이때 \(G_A=A\cap G\), \(H_A=A\cap H\)라 하면 \[G_A\cap H_A=\varnothing \ \Rightarrow \ G_A\subset A\cap H^c\]이고 \(H^c\)은 닫힌 집합이므로 \(\bar{G_A}=A\cap \bar G\subset A\cap H^c\)이 성립한다. 따라서 \(\bar{G_A}\cap H_A= \varnothing\)이다.
(\(\Leftarrow\)) \(G\)와 \(H\)가 공집합이 아닌 서로 분리된 집합이라 하고, \(A=G\cup H\)라 하자. 그러면 \[G\cap \bar H=\varnothing, \ \ \bar G\cap H=\varnothing \ \Rightarrow \ G\subset (\bar H)^c, \ \ H\subset (\bar G)^c\]이므로 \(A\cap (\bar G)^c=H\), \(A\cap (\bar H)^c=G\)이므로 \((\bar G)^c\)와 \((\bar H)^c\)는 \(A\)의 비연결을 이룬다.
# ◀ 닫기
위의 정리의 증명과 비슷한 방법으로 다음을 어렵지 않게 얻어낼 수 있다.
[Proposition 1.6]
두 집합 \(A\), \(B\)가 연결집합이고 서로 분리되지 않은 집합일 때, \(A\cup B\)은 연결집합이다.
[Example 1.7]
[Example 1.2]의 두 집합 \(A\), \(B\)는 서로 연결된 집합이고('길연결'을 이용하여 보일 수 있다.) 분리되지 않은 집합이다. 따라서 \(A\cup B\)는 연결집합이다.
연결공간
어떤 위상공간 \(X\)가 그 집합 자체로서 연결집합이면 \(X\)를 연결공간(connected space)이라 한다. 마찬가지로, 그 위상공간이 그 집합 자체로서 비연결집합이면 \(X\)를 비연결공간(disconnected space)이라고 한다. 다음 정리로부터 연결집합은 부분공간의 관점에서 그 자체로 연결공간이 되기 때문에 위상공간의 부분집합인 연결집합이 아니라 그 집합 자체가 위상공간으로서 연결공간이라고 간주하고 내용을 논해도 문제가 없다.
[Theorem 2.0]
위상공간 \((X, \mathcal T)\)의 부분집합을 \(A\)라 하자. 집합 \(A\)가 \(\mathcal T\)에서 연결된 집합일 필요충분조건은 \(A\)가 \(\mathcal T_A\)에서 연결된 집합인 것이다.
위 정리의 증명은 부분공간 \(A\)의 열린 집합은 위상공간 \(X\)의 열린 집합 \(G\)에 대하여 \(A\cap G\)의 형태로 표현된다는 것을 이용하면 쉽게 증명할 수 있다. 다만, 위 정리가 연결공간의 부분공간이 연결공간이라던가 비연결공간의 부분공간이 비연결공간이라는 것은 아니다.
[Example 2.1]
집합 \(X=\{a, b, c, d, e\}\) 위의 위상 \(\mathcal T=\{X,\, \varnothing, \, \{a\}, \, \{c, d\}, \, \{a, c, d\}, \, \{b, c, d, e\}\}\)에 대하여 위상공간 \(X\)는 비연결공간이다. \(\{a\}\)와 \(\{b, c, d, e\}\)가 \(X\)의 비연결을 이루기 때문이다.
그러나 \(A=\{b, d, e\}\) 위의 부분공간의 위상은 \(\mathcal T_A=\{A, \,\varnothing,\, \{d\}\}\)이므로 \(A\)는 그 부분공간의 두 서로소인 열린 집합의 합집합으로 나타낼 수 없다. 따라서 부분공간 \(A\)는 연결공간이다.
또한 [Theorem 2.0]에서 확장하여, 연결공간의 특성을 다음 정리로 요약할 수 있다.
[Theorem 2.2]
다음 두 가지는 위상공간 \(X\)가 연결공간인 것과 필요충분조건이다.
(i) 집합 \(X\)는 서로소인 두 열린 집합의 합집합으로 나타낼 수 없다.
(ii) \(X\)의 열린 닫힌 집합(clopen set)은 \(X\)와 \(\varnothing\)뿐이다. (Note: 열린 닫힌 집합은 열린 집합이면서 닫힌 집합인 집합이다.)
# 증명 ▶
(Proof)
(i)은 연결집합의 정의로부터 자명하다. 이제 \(X\)가 연결공간인 것이 (ii)와 필요충분조건인 것을 보이자. 이를 증명하기 위해서는 본 명제의 대우를 이용하면 된다.
(\(\Rightarrow\)) 위상공간 \(X\)에 \(X\)와 \(\varnothing\)이 아닌 열린 닫힌 집합 \(G\)가 존재한다고 하자. 그러면 \(G\)와 \(G^c\)는 공집합이 아닌 열린 집합이고, \[G\cap G^c=\varnothing, \ \ G\cup G^c=X\]이므로 \(G\)와 \(G^c\)가 \(X\)의 비연결을 이룬다. 따라서 \(X\)는 비연결공간이다.
(\(\Leftarrow\)) 위상공간 \(X\)가 비연결공간이라고 하자. 그러면 두 서로소인 공집합이 아닌 열린 집합 \(G, \ H\)가 존재하여 \(G\cup H=X\)를 만족시킨다. 따라서 \(H=G^c\)이므로 \(G, \ H\)는 공집합도 아니고 \(X\)도 아닌 열린 닫힌 집합이다.
# ◀ 닫기
[Example 2.3]
\(\Bbb R\)의 보통 위상공간은 연결공간이다. \(\Bbb R\)의 열린 닫힌 집합은 \(\Bbb R\)과 \(\varnothing\)뿐이기 때문이다.
연결성은 연속성과도 관련이 있다. 연속성은 열린 집합의 성질을 대부분 유지하기 때문에 연결집합의 연속함수에 의한 상도 연결집합이 된다. 후에 언급하겠지만, \(\Bbb R\)에서의 사잇값 정리(Intermediate Value Theorem)가 이 성질을 보여주는 대표적인 정리이다.
[Theorem 2.4]
연결집합의 연속함수에 의한 상은 연결집합이다.
# 증명 ▶
(Proof)
\(X\)가 연결공간이고 \(Y\)가 위상공간일 때, \(f: X\to Y\)를 연속함수라고 하자. \(f[X]\)가 비연결집합이라고 가정하자. 그러면 서로소인 \(Y\)의 열린 집합 \(G\), \(H\)가 존재하여 \(f[X]=G\cup H\)를 만족시킨다. \(f\)는 연속함수이므로 \(f^{-1}[G]\)와 \(f^{-1}[H]\)는 \(X\)의 열린 집합이고, \[f^{-1}[G\cup H]=f^{-1}[G]\cup f^{-1}[H]=X\]이므로 \(X\)는 비연결공간이 된다. 이는 모순이다. 따라서 \(X\)가 연결집합이면 \(f[X]\)도 연결집합이다.
# ◀ 닫기
위 정리의 자명한 결과로 다음을 얻을 수 있다.
[Corollary 2.5]
위상공간 \(X\)가 연결공간일 필요충분조건은 \(X\)에서 이산 위상공간 \(Y=\{0, 1\}\)로의 연속함수는 상수함수뿐인 것이다.
한편, 실수 전체의 집합 \(\Bbb R\) 위의 보통 위상공간에서의 연결집합은 '구간'이라는 특성으로 나타난다. 일반적으로 구간이란 다음과 같이 정의할 수 있다. (책마다 다르지만, 우리 책에서는 다음과 같이 서술하고 있다.)
[Definition 2.6]
\(\Bbb R\)의 부분집합 \(I\)가 임의의 \(a, b\in I\)에 대하여 \(a<x<b\)이면 \(x\in E\)를 만족시키면 \(I\)를 구간(interval)이라 한다.
위에서 언급한 것과 같이 \(\Bbb R\)의 연결집합은 구간과 같다. 이는 실해석학의 여러 정리에 응용될 수 있는 유용한 성질이다.
[Theorem 2.7]
\(\Bbb R\)의 부분집합 \(I\)가 적어도 두 개의 원소를 가지고 있다고 하자. \(I\)가 연결집합일 필요충분조건은 \(I\)가 구간인 것이다.
# 증명 ▶
(Proof)
(\(\Rightarrow\)) \(I\)가 구간이 아니라고 하자. 그러면 어떤 \(a,\, b\in I\)와 \(a<x<b\)인 \(x\in \Bbb R\)에 대하여 \(x\notin I\)이다. 그러면 \((-\infty, \, x)\)와 \((x, \, \infty)\)는 \(I\)의 비연결을 이루므로 \(I\)는 비연결집합이다.
(\(\Leftarrow\)) \(I\)가 구간이지만 비연결집합이라고 하고, \(G\cup H\)를 \(I\)의 비연결이라 하자. 일반성을 잃지 않고, \(a\in G\), \(b\in H\), \(a<b\)라 하면 상한 공리에 의하여 \(c=\sup ([a, b]\cap G)\)가 존재한다. 구간의 정의로부터 \(c\in I\)이고 \(G, \, H\)가 \(I\)의 비연결이므로 \(c\in G\) 또는 \(c\in H\)이다.
\(c\in G\)라 하면 \(c\)는 \(G\)의 내점이므로 \((c-\epsilon, \, c+\epsilon)\subset G\)인 \(\epsilon>0\)이 존재한다. 그러면 \(c+\epsilon/2\in G\)이므로 \(c=\sup ([a, b]\cap G)\)라는 데에 모순이다.
\(c\in H\)라 하면 \(c\)는 \(H\)의 내점이므로 \((c-\delta, \, c+\delta)\subset H \; \cdots (*)\)인 \(\delta>0\)이 존재한다. 또한 \(c\notin G\)이므로 \(c\)의 정의로부터 \(c-\delta<x_0<c\)인 \(x_0\in G\)가 존재한다. 이때 \((*)\)에 의하여 \(x_0\in H\)이다. 이는 모순이다.
따라서 \(I\)가 구간이면 \(I\)는 연결집합이다.
# ◀ 닫기
위 정리의 결과로 일반화된 사잇값의 정리를 얻을 수 있다.
[Theorem 2.8] (Generalized IVT: 일반화된 사잇값 정리)
연결집합 \(X\)에서 정의된 연속함수 \(f: X\to \Bbb R\)와 임의의 \(p, q\in X\)에 대하여 함수 \(f\)는 \(f(p)\)와 \(f(q)\) 사이의 모든 값을 취한다. 즉, \(f(p)\)와 \(f(q)\) 사이의 임의의 실수 \(k\)에 대하여 \(f(c)=k\)인 \(c\in X\)가 존재한다.
# 증명 ▶
(Proof)
\(X\)는 연결집합이고 \(f\)는 연속함수이므로 [Theorem 2.4]에 의하여 \(f[X]\)는 연결집합이다. \(f[X]\in \Bbb R\)이므로 [Theorem 2.7]에 의하여 \(f[X]\)는 구간이다. 따라서 주어진 정리가 성립한다.
# ◀ 닫기
Reference: <SCHAUM'S outlines: General Topology>, Seymour Lipschutz.
'[Undergraduates] > 위상수학' 카테고리의 다른 글
| [Chapter 13] 연결성 - (2) (2) | 2021.06.09 |
|---|---|
| [Chapter 12] 곱공간 (0) | 2021.05.09 |
| [Chapter 11] 컴팩트성 - (2) (2) | 2021.04.27 |