컴팩트화
일반적인 위상 공간은 점을 추가하여 컴팩트공간으로 만들 수 있다. 이를 컴팩트화라고 한다. 대표적으로 복소함수론에서 다루는 \(\Bbb C\)의 컴팩트화가 있다.
[Example 0.0]
그림과 같이 구 \(S: x^2+y^2+(z-1)^2=1\) 위의 점 \((0, 0, 2)\)와 \(xy\)평면 위의 한 점 \(p\)를 지나는 직선을 그리면 그 직선과 구 \(S\)는 한 점 \(p'\)에서만 만난다. 이를 이용하면 복소평면 \(\Bbb C\)의 임의의 점과 구 \(S\) 위의 한 점은 일대일대응이 됨을 알 수 있다. 이때 구 위의 점 \((0, 0, 2)\)와 대응되는 점을 \(\infty\)라고 하자. 이때 함수 \(f: \Bbb S \to \Bbb C\cup \{\infty\}\)를 \(f(p')=p\)라 하면 \(f\)는 일대일대응이고 실제로는 위상동형사상이 된다. 이때 \(S\)는 컴팩트하므로 \(\Bbb C\cup \{\infty\}\)는 컴팩트하다. (이때 \(\Bbb C\)는 컴팩트하지 않다는 데에 주목하자.)
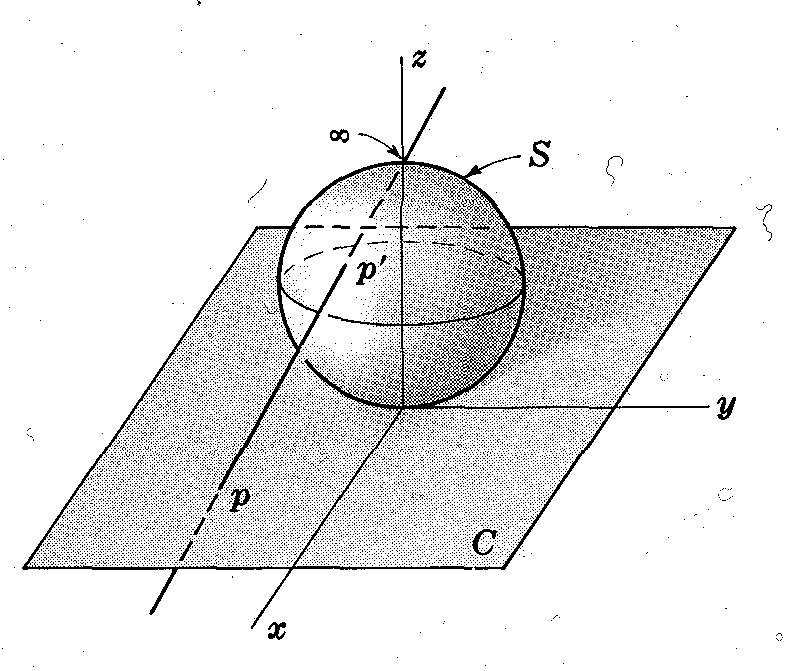
이런 식으로 점을 추가하여 위상공간을 컴팩트공간으로 만드는 것을 한 점 컴팩트화라고 한다.
[Theorem 0.1]
위상공간 \((X, \mathcal T)\)에 대하여 다음과 같이 정의된 위상공간 \((X_{\infty}, \mathcal T_{\infty})\)는 컴팩트공간이다.
(1) \(X_{\infty}=X\cup \{\infty\}\,\)이고 \(\infty\)는 \(X\)의 모든 점과 다른 점이다.
(2) \(\mathcal T_{\infty}\)의 원소는 다음 둘 중 하나이다.
(i) \(\mathcal T\)의 모든 원소
(ii) \(X\)의 컴팩트한 닫힌 집합의 \(X_{\infty}\)에서의 여집합
이렇게 생성된 위상 \((X_{\infty}, \mathcal T_{\infty})\)을 알렉산드로프 컴팩트화(Alexandrov compactification) 또는 한 점 컴팩트화(One-point compactification)라고 한다.
# 증명 ▶
(Proof)
(1) 우선 \((X_{\infty}, \mathcal T_{\infty})\)이 위상공간임을 보이자.
\(\mathbf {[T_1]}\) \(\varnothing\in \mathcal T\)이므로 \(\varnothing \in \mathcal T_{\infty}\)이다. 또한 \(\varnothing\)은 \(X\)의 닫힌 컴팩트집합이므로 \(\varnothing^c=X_{\infty}\in \mathcal T_{\infty}\)이다.
\(\mathbf {[T_2]}\) \(G, \, H\in \mathcal T_{\infty}\)라 하자.
(i) \(G, \, H\in \mathcal T\)이면 \(G\cap H\in \mathcal T\)이므로 \(G\cap H\in \mathcal T_{\infty}\)이다.
(ii) \(G\in \mathcal T\)이고 \(H\notin \mathcal T\)이면 \(X-G\)와 \(X_\infty-H\)은 \(X\)의 닫힌 부분집합이므로 \((X-G)\cup (X_\infty-H)\)는 \(X\)의 닫힌 부분집합이다. 또한 \(\infty \notin G\)이므로 \(\infty \notin G\cap H\)이다. 즉, \(G\cap H\subset X\)이므로 \(G\cap H=X-\{(X-G)\cup (X_\infty-H)\}\in \mathcal T\)이다. 따라서 \(G\cap H\in \mathcal T_{\infty}\)이다.
(iii) \(G\notin \mathcal T\)이고 \(H\notin \mathcal T\)인 경우 \(X_\infty-G\)와 \(X_\infty-H\)는 \(X\)의 닫힌 컴팩트 부분집합이다. 따라서 \((X_\infty-G)\cup (X_\infty-H)\)도 \(X\)의 닫힌 컴팩트 부분집합이므로 \(G\cap H=X_\infty-\{(X_\infty-G)\cup (X_\infty-H)\}\in \mathcal T_{\infty}\)이다.
\(\mathbf {[T_3]}\) \(\{G_i\}\)를 \(\mathcal T_{\infty}\)의 원소들의 집합이라고 하자.
(i) \(\infty\in \bigcup_i G_i\)인 경우, \[\{G_i\}=\{G_{i_\alpha}: \forall \alpha, \, \infty\in G_{i_\alpha}\}\cup\{G_{i_\beta}: \forall \beta, \, \infty\notin G_{i_\beta}\}\]와 같이 표현할 수 있다. 이때 각 \(\alpha, \, \beta\)에 대하여 \(X_\infty-G_{i_\alpha}\)는 \(X\)의 닫힌 컴팩트 부분집합이고 \(X-G_{i_\beta}\)는 \(X\)의 닫힌 부분집합이므로 \[\bigcap_i (X_\infty-G_i)=\displaystyle \left(\bigcap(X_\infty-G_{i_\alpha}\right) \cap \left(\bigcap(X-G_{i_\beta})\right)\]는 \(X\)의 닫힌 컴팩트 부분집합이다. 따라서 \(\bigcup_i G_i=X_{\infty}-\displaystyle \bigcap_i (X_\infty-G_i)\in \mathcal T_{\infty}\)이다.
(ii) \(\infty \notin \bigcup_i G_i\)인 경우, 모든 \(\{G_i\}\)의 원소는 \(\mathcal T\)의 원소이므로 \(\bigcup_i G_i\in \mathcal T\)이다. 따라서 \(\bigcup_i G_i\in \mathcal T_{\infty}\)이다.
(2) \(\mathbf {[T_1], \, [T_2], \, [T_3]}\)에서 \((X_{\infty}, \mathcal T_{\infty})\)는 위상공간이다. 이제 \(X_{\infty}\)가 컴팩트공간임을 보이자. \(\{B_i\}\)를 \(X_{\infty}\)의 한 열린 덮개라고 하자. 그러면 \(\infty\in B_{i_0}\)인 \(B_{i_0}\in \{B_i\}\)가 존재한다. 이 공간의 정의에 의하여 \(B_{i_0}^c\)은 \(X\)의 컴팩트한 부분집합이다. 따라서 \(\{B_i\}\)의 유한개의 원소 \(B_{i_1}, \, B_{i_2}, \, \cdots, \, B_{i_m}\)이 존재하여 \[B_{i_0}^c\subset B_{i_1}\cup B_{i_2}\cup \cdots \cup B_{i_m}\]을 만족시킨다. 따라서 \(\{B_{i_0}, \, B_{i_1}, \, B_{i_2}, \, \cdots, \, B_{i_m}\}\)은 \(\{B_i\}\)의 유한 부분덮개이다. 따라서 \(X_{\infty}\)는 컴팩트공간이다.
# ◀ 닫기
한 점 컴팩트화는 기존의 공간에 한 점을 추가해서 만든 것이므로 기존의 공간의 성질을 대부분 그대로 가진다. 대표적으로 하우스도르프 공간과 관련된 다음의 성질이 있다.
[Definition 0.2]
위상공간 \(X\)의 각 점 \(p\)가 컴팩트한 근방을 가지면, 즉, 임의의 \(p\in X\)에 대하여 \(p\)를 포함하는 컴팩트한 집합 \(C_p\)와 열린 집합 \(G_p\)가 존재하여 \(p\in G_p \subset C_p\)를 만족시키면 \(X\)를 국소 컴팩트 공간(locally compact space)이라고 한다.
[Theorem 0.3]
위상공간 \((X, \mathcal T)\)가 국소 컴팩트인 하우스도르프 공간이면 \((X_{\infty}, \mathcal T_{\infty})\)는 하우스도르프 컴팩트 공간이다. (따라서 정규 공간이다.)
# 증명 ▶
(Proof)
컴팩트화의 성질로부터 \((X_{\infty}, \mathcal T_{\infty})\)는 컴팩트공간이다. \(X\)는 하우스도르프 공간이므로 \(p, q\in X\)이면 \(p\in G, \, q\in H\)이고 \(G\cap H=\varnothing\)인 두 열린 집합 \(G, \, H\)가 존재한다. \(p\in X\)이고 \(q=\infty\)인 경우, \(X\)는 국소 컴팩트 공간이므로 \(p\in G_p\subset C_p\)인 열린 집합 \(G_p\)와 컴팩트집합 \(C_p\)가 존재한다. 하우스도르프 공간에서 컴팩트집합은 닫힌 집합이므로 \(C_p\)는 \(X\)의 컴팩트한 닫힌 집합이다. 따라서 \(C_p^c\in \mathcal T_{\infty}\)이다. 이때 \[p\in G_p, \ \ q\in C_p^c, \ \ G_p\cap C_p^c=\varnothing\]이다. 따라서 \((X_{\infty}, \mathcal T_{\infty})\)은 하우스도르프 공간이다.
# ◀ 닫기
거리공간과 컴팩트성
거리공간의 대표적 예로 \(\Bbb R\)을 생각해보면, 볼차노-바이어슈트라스 정리에 의하여 \(\Bbb R\)의 유계인 무한집합은 집적점을 가지고, 유계인 수열은 수렴하는 부분수열을 가진다. 특히, 집합을 닫힌 집합으로 한정하면 그 집적점이 그 닫힌 부분집합 내에 존재하게 된다. 이와 비슷하게 거리 공간은 앞에서 다룬 컴팩트, 극한점 컴팩트, 점열 컴팩트가 모두 동치가 된다.
앞의 논의에서 [컴팩트 \(\Rightarrow\) 극한점 컴팩트]인 것과 [점열 컴팩트 \(\Rightarrow\) 극한점 컴팩트]인 것은 보였으므로 거리공간에서는 [극한점 컴팩트 \(\Rightarrow\) 점열 컴팩트]와 [점열 컴팩트 \(\Rightarrow\) 컴팩트]임을 증명할 것이다. 전자의 경우 어렵지 않게 보일 수 있지만, 후자의 경우 증명하기 위해 '완전 유계'와 '르벡 수'를 이용한다.
[Theorem 1.0]
위상공간 \(X\)가 거리 공간이고 극한점 컴팩트 공간이면 \(X\)는 점열 컴팩트 공간이다.
# 증명 ▶
(Proof)
수열 \(\{x_n\}\)을 \(X\) 위의 임의의 수열이라고 하자.
(1) 집합 \(\{x_n\mid n\in \Bbb N\}\)이 유한집합인 경우, \(n_0\in \Bbb N\)이 존재하여 \(n>n_0\)일 때마다 \(x_n=p\)인 \(p\in X\)가 존재한다. 따라서 수열 \(\{x_n\}\)은 \(p\)로 수렴하는 부분수열을 갖는다.
(2) 집합 \(\{x_n\mid n\in \Bbb N\}\)이 무한집합인 경우, \(X\)는 극한점 컴팩트 공간이므로 집합 \(\{x_n\mid n\in \Bbb N\}\)은 \(X\) 위에서 집적점 \(p\)를 갖는다. \(X\)는 거리 공간이므로 자연수 \(k\)에 대하여 \(x_{n_k}\in S(p, \, 1/k)\)인 \(x_{n_k}\in \{x_n\}\)이 존재한다. 이렇게 구성된 수열 \(\{x_{n_k}\}\)는 \(p\)로 수렴하는 수열 \(\{x_n\}\)의 부분수열이다.
(1), (2)로부터 \(X\)는 점열 컴팩트 공간이다.
# ◀ 닫기
이제 점열 컴팩트인 거리 공간은 컴팩트공간인 것을 보일 것이다. 이는 점열 컴팩트 거리공간이 충분히 '성긴' 공간이라는 점에서 기인한다. 즉, 점열 컴팩트 거리공간의 점들은 모두 유한개의 점들에 주변에 몰려 있다. 직관적으로 유한 개의 점들의 '덩어리'로 이루어져 있다고 생각하면 된다. 이러한 성질을 갖는 집합을 완전 유계 집합이라고 한다.
[Definition 1.1]
(1) 집합 \(A\)를 거리공간 \(X\)의 부분집합이라고 하자. 양수 \(\epsilon\)와 \(X\)의 유한개의 점들의 집합 \[N=\{e_1, \, e_2, \, \cdots, \, e_m\}\]에 대하여 임의의 \(p\in A\)에 대하여 \(e_{i_0}\in N\)가 존재하여 \(d(p, \,e_{i_0})<\epsilon\)을 만족시키면 집합 \(N\)을 집합 \(A\)의 \(\epsilon-\)그물 (\(\epsilon-\)net)이라 한다.
(2) 거리공간 \(X\)의 부분집합 \(A\)가 임의의 \(\epsilon>0\)에 대하여 \(\epsilon-\)그물을 가지면 \(A\)를 완전 유계 집합(totally bounded set)이라 한다.
점열 컴팩트 공간은 임의의 집합 위에서의 수열이 수렴하는 부분수열을 갖는 공간이므로 그 수렴하는 점 주변에 많은 점들이 몰려 있다. 한 공간에서 셀 수 없을 정도로 많은 점들로 수렴하는 무수히 많은 수열을 잡을 수는 없을 것이므로, 점열 컴팩트 공간이 완전 유계 공간이 될 것이라는 점을 추측할 수 있다.
[Theorem 1.2]
거리공간 \(X\)의 부분집합 \(A\)가 점열 컴팩트 집합이라고 하자. 그러면 \(A\)는 완전 유계 집합이다.
# 증명 ▶
(Proof)
거리공간 \(X\)의 부분집합 \(A\)가 점열 컴팩트 집합이지만 완전 유계 집합이 아니라고 하자.
임의의 \(\epsilon>0\)에 대하여 \(a_1\in A\)를 택하자. 그러면 \(d(a_1, \, a_2)\geq \epsilon\)인 \(a_2\in A\)가 존재한다. 그렇지 않으면 \(\{a_1\}\)이 \(A\)의 \(\epsilon-\)그물이 되기 때문이다. 비슷한 방법으로 \(d(a_1, \, a_3)\geq \epsilon\)이고 \(d(a_2, \, a_3)\geq \epsilon\)인 \(a_3\in A\)가 존재한다. 그렇지 않으면 \(\{a_1, \, a_2\}\)가 \(A\)의 \(\epsilon-\)그물이 되기 때문이다.
이러한 방식으로 자연수 \(n(\geq 2)\)에 대하여 \(d(a_i, \, a_n)\geq \epsilon \; (i=1, \,2, \,\cdots,\, n-1)\)인 \(a_n\in A\)가 존재한다. 이렇게 정의된 수열 \(\{a_n\}\)은 \(A\) 위의 수열이지만 모든 점 사이의 거리가 \(\epsilon\)보다 크거나 같으므로 \(A\) 위의 어느 점으로도 수렴하지 않는다. 이는 가정에 모순이므로 \(A\)는 완전 유계 집합이다.
# ◀ 닫기
완전 유계 집합은 성긴 집합이지만, 컴팩트공간만큼 그렇지는 않다. 컴팩트공간은 '임의의' 열린 덮개가 유한 개의 부분덮개를 가져야 하므로 유한개의 점에 점들의 덩어리가 몰려 있는 완전 유계 공간보다 더 강력한 조건이 필요하다. 그것을 덮개의 '르벡 수'를 이용하여 설명한다.
[Definition 1.3]
\(\mathscr A=\{G_i\}\)를 거리 공간 \(X\)의 부분집합 \(A\)의 한 덮개라고 하자. 양수 \(\delta\)에 대하여 지름(diameter)이 \(\delta\)보다 작은 임의의 \(A\)의 부분집합을 포함하는 \(G_{i_0}\in \mathscr A\)가 존재하면 \(\delta\)를 덮개 \(\mathscr A\)의 르벡 수(Lebesgue number)라고 한다.
완전 유계 집합의 덮개가 르벡 수를 가지게 되면, 완전 유계 집합의 그물과 르벡 수를 이용하면 유한개의 부분 덮개를 만들 수 있을 것이다. 이를 이용하면 다음 정리를 이끌어낼 수 있다.
[Theorem 1.4]
거리공간의 임의의 점열 컴팩트 부분집합의 모든 열린 덮개는 (양수인) 르벡 수를 갖는다.
# 증명 ▶
(Proof)
거리공간 \(X\)의 점열 컴팩트 부분집합 \(A\)에 대하여 \(A\)의 열린 덮개 \(\{G_i\}\)가 르벡 수를 갖지 않는다고 가정하자. 그러면 자연수 \(n\)에 대하여 \[d(B_n)<1/n, \ \ \forall i: B_n\not \subset G_i \ \ \cdots \; (*)\]인 \(B_n\subset A\)가 존재한다. 이때 \(b_n\in B_n\)을 선택하면, \(A\)는 점열 컴팩트 집합이므로 수열 \(\{b_n\}\)은 \(p\in A\)로 수렴하는 부분수열 \(\{b_{n_k}\}\)가 존재한다. 또한 \(p\in A\)이므로 \(p\)를 포함하는 열린 덮개 \(\{G_i\}\)의 원소 \(G_{i_0}\)가 존재한다. \(p\)는 \(G_{i_0}\)의 내점이므로 \[p\in S(p, \, \epsilon)\subset G_{i_0}\]인 \(\epsilon>0\)이 존재한다. 이때 \(\{b_{n_k}\}\)는 \(p\)로 수렴하고 \(d(B_{n_k})<1/n_k\)이므로 아르키메데스 원리에 의하여 \[d(B_{n_{k_0}})<\epsilon/2, \ \ d(b_{n_{k_0}}, \, p)<\epsilon/2\]인 \(n_{k_0}\in \Bbb N\)이 존재한다. 이때 임의의 \(x\in B_{n_{k_0}}\)에 대하여 \[d(x, p)\leq d(x, b_{n_{k_0}})+d(b_{n_{k_0}}, p)<\epsilon/2+\epsilon/2=\epsilon\]이므로 \(x\in S(p, \, \epsilon)\)이다. 즉, \(B_{n_{k_0}}\subset S(p,\, \epsilon)\subset G_{i_0}\)이고 이는 \((*)\)에 모순이다. 따라서 거리 공간의 점열 컴팩트 부분집합의 모든 열린 덮개는 르벡 수를 갖는다.
# ◀ 닫기
이제 점열 컴팩트 거리 공간은 컴팩트공간임을 증명할 수 있다. 위에서 언급했던 것과 같이 완전 유계의 성질과 르벡 수를 이용하면 된다.
[Theorem 1.5]
위상공간 \(X\)가 거리 공간이고 점열 컴팩트이면 \(X\)는 컴팩트공간이다.
# 증명 ▶
(Proof)
\(\mathcal G=\{G_i\}\)를 \(X\)의 임의의 열린 덮개라고 하자. [Theorem 1.4]에 의하여 \(\mathcal G\)는 르벡 수 \(\delta>0\)을 갖는다. 또한 [Theorem 1.2]에 의하여 \(X\)는 완전 유계 집합이므로 \(X\)는 \(\delta-\)그물 \(N=\{e_1, \, e_2, \, \cdots, \, e_m\}\)을 갖는다. 그물의 정의에 의하여 집합 \(S=\{S(e_1, \delta), \, S(e_2, \delta), \, \cdots, \, S(e_m, \delta)\}\)은 \(X\)의 열린 덮개이다. 또한 르벡 수의 정의에 의하여 각 \(k=1, \, 2, \, \cdots, \, m\)에 대하여 \(S(e_k, \delta)\subset G_{i_k}\)인 \(G_{i_k}\in \mathcal G\)가 존재한다. 따라서 \[X\subset \displaystyle \bigcup_{k=1}^m S(e_k, \delta)\subset \bigcup_{k=1}^m G_{i_k}\]이므로 \(\{G_{i_1}, \, G_{i_2}, \, \cdots, \, G_{i_m}\}\)은 \(\mathcal G\)의 유한 부분덮개이다. 따라서 \(X\)는 컴팩트공간이다.
# ◀ 닫기
위의 논의로부터 거리 공간에서의 컴팩트성에 대하여 다음 결론이 성립한다.
[Theorem 1.6]
\(X\)가 거리 공간이라고 하자. 그러면 다음은 모두 동치이다.
(1) \(X\)가 컴팩트공간이다.
(2) \(X\)가 점열 컴팩트 공간이다.
(3) \(X\)가 극한점 컴팩트 공간이다.
여러 가지 문제들
[Problem 2.0]
함수 \(f:X \to Y\)를 연속함수라고 하자.
(1) \(A\subset X\)가 점열 컴팩트 집합이면 \(f[A]\)도 점열 컴팩트 집합임을 보여라.
(2) \(A\subset X\)가 극한점 컴팩트 집합이지만 \(f[A]\)는 극한점 컴팩트 집합이 아닌 예를 들어라.
# 증명 ▶
(Proof)
(1) 수열 \(\{a_n\}\)을 \(f[A]\) 위의 한 수열이라고 하자. 그러면 \(a_n=f(b_n)\)인 \(b_n\in A\)가 존재한다. \(A\)가 점열 컴팩트 집합이므로 \(A\) 위의 점 \(p\)로 수렴하는 \(\{b_n\}\)의 부분수열 \(\{b_{n_i}\}\)가 존재한다. 이때 연속함수는 점열 연속함수이므로 \(\{a_{n_i}\}=\{f(b_{n_i})\}\)는 \(f(p)\)로 수렴하는 \(\{a_n\}\)의 부분수열이다. 따라서 \(f[A]\)는 점열 컴팩트이다.
(2) \(\Bbb N\) 위의 위상 \(\mathcal T\)를 집합 \(\mathcal B=\{\{2n-1, \, 2n\} \mid n\in \Bbb N\}\)를 기저로 갖는 위상이라고 하자. 이때 \(\Bbb N\)은 모든 자연수를 집적점으로 갖는 극한점 컴팩트 집합이다. 이때 함수 \(f:(\Bbb N, \, \mathcal T) \to (\Bbb N, \, \mathfrak D)\)를 \(f(2n-1)=f(2n)=n, \; \forall n\in \Bbb N\)이라 하자. 그러면 \(f\)는 연속함수이지만 \((\Bbb N, \, \mathfrak D)\)는 극한점 컴팩트 집합이 아니다.
[Note] 위의 \(\Bbb N\) 위로의 위상 \(\mathcal T\)는 극한점 컴팩트와 관련된 중요한 반례로 기억해두는 것이 좋다.
# ◀ 닫기
[Problem 2.1]
위상공간 \((X, \mathcal T)\)를 여가산위상(cocountable topology)이라 하자. 이때 \(X\)의 임의의 무한 부분집합은 점열 컴팩트가 아님을 보여라.
# 증명 ▶
(Proof)
\(A\subset X\)를 무한집합이라 하고, \(\{x_n\}\)을 \(A\) 위의 임의의 수열이라고 하자. \(\{x_n\}\)이 \(p\in A\)로 수렴하는 부분수열 \(\{x_{n_i}\}\)를 갖는다고 하면 \(p\in A\)를 포함하는 임의의 열린 집합 \(G_p\)는 수열 \(\{x_{n_i}\}\)의 유한개를 제외한 모든 항을 포함해야 한다. 이때 \[G_p^*=G_p \, \backslash \, (\{x_{n_1}, \, x_{n_2}, \, \cdots, \, x_{n_i}, \, \cdots\} \backslash \{p\})\]는 여가산위상의 정의에 의하여 \(p\)를 포함하는 열린 집합이다. 그러나 \(G_p^*\)는 \(p\)를 제외하면 수열 \(\{x_{n_i}\}\)의 단 하나의 항도 포함하지 않는다. 따라서 \(X\)의 임의의 무한 부분집합은 점열 컴팩트가 아니다.
# ◀ 닫기
[Problem 2.2]
함수 \(f\)를 컴팩트 거리공간 \((X, d)\)에서 거리공간 \((Y, d^*)\)로의 연속함수라고 하자. 그러면 \(f\)는 균등연속임을 보여라. 즉, 임의의 \(\epsilon>0\)에 대하여 \(\delta>0\)이 존재하여 \[d(x, y)<\delta \; \Rightarrow \; d^*(f(x), \,f(y))<\epsilon\]을 만족시킴을 보여라.
# 증명 ▶
(Proof)
함수 \(f\)는 연속이므로 임의의 \(p\in X\)와 \(\epsilon>0\)에 대하여 \[d(x, p)<\delta_p \; \Rightarrow \; d^*(f(x), f(p))<\epsilon/2\]을 만족시키는 \(\delta_p>0\)가 존재한다. 이때 \(\{S_d(p,\, \delta_p) \mid p\in X\}\)는 \(X\)의 열린 덮개이고 \(X\)는 컴팩트공간이므로 르벡 수 \(\delta>0\)이 존재한다. 즉, \(d(x, y)<\delta\)라 하고 \(A=\{x, y\}\)라 하면 \(d(A)<\delta\)이므로 \(A\subset S_d(p_0, \, \delta_{p_0})\)인 \(p_0\in X\)가 존재한다. 따라서 \(d(x, p)<\delta_{p_0}\)이고 \(d(y, p)<\delta_{p_0}\)이므로 \[\begin{align}d^*(f(x), \, f(y))&\leq d^*(f(x), \, f(p))+d^*(f(p), \, f(y))\\[.4em]&<\epsilon/2+\epsilon/2=\epsilon\end{align}\]이다. 즉, \(d(x, y)<\delta\)일 때마다 \(d^*(f(x), \, f(y))<\epsilon\)이므로 \(f\)는 균등연속이다.
# ◀ 닫기
[Problem 2.3]
\(X\)를 제2가산공간이면서 \(T_1-\)공간이라고 하자. 이때 \(X\)가 컴팩트일 필요충분조건이 \(X\)가 극한점 컴팩트인 것임을 보여라.
# 증명 ▶
(Proof)
\(X\)가 컴팩트이면 \(X\)는 극한점 컴팩트임을 이미 보인 바 있다. 역으로 \(X\)가 극한점 컴팩트라고 하자. \(X\)가 제2가산공간이므로 \(X\)는 린델뢰프 공간이다. 즉, 임의의 열린 덮개는 가산인 부분 덮개를 갖는다. 또한 \(X\)가 \(T_1-\)공간이므로 \(X\)가 극한점 컴팩트이면 \(X\)는 가산 컴팩트이다. 즉, 모든 가산인 부분 덮개는 유한인 부분 덮개를 갖는다. 따라서 \(X\)의 임의의 열린 덮개는 유한인 부분 덮개를 갖는다. 이로부터 \(X\)는 컴팩트 공간이 된다.
# ◀ 닫기
[Problem 2.4]
\(A\)를 거리공간 \(X\)의 컴팩트한 부분집합이라 하자. 이때 \(A\)의 도집합 \(A'\)는 컴팩트집합임을 보여라.
# 증명 ▶
(Proof)
우선 \(A'\)이 닫힌 집합임을 보이자. \(\alpha\)를 \(A'\)의 집적점이라고 하자. \(X\)가 거리 공간이므로 모든 자연수 \(n\)에 대하여 \(\alpha_n\in S(\alpha, \, 2^{-n})\)인 \(\alpha_n\in A'\)이 존재한다. 또한 \(\alpha_n\in A'\)이므로 \(x_n\in S(\alpha_n, \, 2^{-n})\)인 \(x_n\in A\)가 존재한다. 따라서 \[d(x_n,\, \alpha)\leq d(x_n, \,\alpha_n)+d(\alpha_n,\, \alpha)<2^{-n}+2^{-n}=2^{1-n}\]이므로 \(x_n\in S(\alpha, \, 2^{1-n})\)인 \(x_n\in A\)가 존재한다. 즉, \(\alpha\)는 \(A\)의 집적점이므로 \(\alpha\in A'\)이다. \(\alpha\)는 임의로 선택된 집적점이므로 \(A'\)는 닫힌 집합이다.
한편, 거리 공간은 하우스도르프 공간이므로 \(A\)는 \(X\)의 닫힌 부분집합이다. \(A'\)은 \(X\)의 닫힌 부분집합이므로 그 부분공간인 \(A\)의 닫힌 부분집합이다. 부분공간 \(A\)는 컴팩트공간이므로 그 닫힌 부분집합인 \(A'\)은 컴팩트집합이다.
# ◀ 닫기
Reference: <SCHAUM'S outlines: General Topology>, Seymour Lipschutz.
'[Undergraduates] > 위상수학' 카테고리의 다른 글
| [Chapter 12] 곱공간 (0) | 2021.05.09 |
|---|---|
| [Chapter 11] 컴팩트성 - (1) (0) | 2021.04.16 |
| [Chapter 10] 분리 공리 (2) - Problems (0) | 2021.04.10 |