코시의 정리
코시의 정리 또는 코시-구르사(Cauchy-Goursat)의 정리라 불리는 정리는 복소해석학의 가장 중심적이고 핵심적인 정리 중 하나이다. 이로부터 코시의 적분 공식, 리우빌 정리, 해석함수의 성질 등 여러 가지를 유도할 수 있다. 얼핏 보면 미적분의 기본 정리와 비슷해 보이지만, 본질적으로 피적분함수의 도함수의 연속성을 가정하지 않는다는 점에서 다르다. 우선 코시의 정리의 진술은 다음과 같다.
[Theorem 6.0] [The Cauchy-Goursat Theorem: 코시-구르사의 정리]
\(\gamma^*\)를 조각마다 매끄러운 함수 \(\gamma: [a, b]\to \Bbb C\)에 의하여 결정되는 폐경로(contour)라 하자. \(D\)를 \(\text{Int}(\gamma)\cup \gamma^*\)를 포함하는 열린 집합이라 하고, \(f\in H(D)\)라 하자. 그러면 \(\int_\gamma f(z)dz=0\)이다.
처음 코시는 이 정리에 대한 증명을 더 강한 전제 조건 아래에서 제시하였다. 즉,
[Theorem 6.1]
\(\gamma^*\)를 조각마다 매끄러운 함수 \(\gamma: [a, b]\to \Bbb C\)에 의하여 결정되는 폐경로(contour)라 하자. \(D\)를 \(\text{Int}(\gamma)\cup \gamma^*\)를 포함하는 열린 집합이라 하고, \(f\in H(D)\)이고 \(\pmb{f'\in C(D)}\)라 하자. 그러면 \(\int_\gamma f(z)dz=0\)이다.
# 증명 ▶
(Proof)
\(z=x+iy\)에 대하여 \(f(z)=u(x, y)+iv(x, y)\)라 하자. 그러면 \(dz=dz+idy\)이므로 다음이 성립한다. \[\begin{align}\int_\gamma f(z)dz&=\int_\gamma (u+iv)(dx+idy)\\[.4em] &=\int_\gamma (udx-vdy)+i\int_\gamma (v dx+udy)\\[.4em] &=\iint_\gamma (-v_x-u_y)dxdy+i\iint_\gamma(u_x-v_y)dxdy \quad \cdots \ \text{(i)}\end{align}\] 이때 코시-리만 방정식에서 \(u_x=v_y, \ u_y=-v_x\)가 성립하므로 위의 식의 값은 \(0\)이 된다. 따라서 \(\int_\gamma f(z)dz=0\)이다.
(Note) 위의 증명에서 \(\text{(i)}\)가 성립하기 위해서는 \(f'\)가 \(D\)에서 연속이라는 조건이 필요하다. (그린 정리)
# ◀ 닫기
구르사는 [Theorem 6.0]과 같이 \(f\)가 \(D\)에서 연속인 도함수를 갖는다는 전제를 제거한 증명을 제시하였다. 그래서 이를 '코시-구르사의 정리'라고 부른다. [Theorem 6.0]의 증명은 \(\text{Int}(\gamma)\cup \gamma^*\)의 형태에 따라 다음과 같은 순서로 전개된다.
(1) 삼각형 모양의 경로
(2) 볼록도형
(3) 다각형(볼록성과 관계 없는)
(4) 일반적인 조각마다 매끄러운 곡선
사실 구르사가 증명한 (1)의 내용이 이 코시의 정리에서 가장 중요하다고 할 수 있다. 나머지는 모두 (1)을 이용한 응용과 그 결과라고 할 수 있기 때문이다.
[Theorem 6.2] (코시의 정리: 삼각형 모양의 경로)
\(\partial \triangle\)을 삼각형 모양의 폐경로라고 하자. \(D\)를 \(\text{Int}(\triangle)\cup \partial \triangle\)을 포함하는 열린 집합이라 하고, \(f\in H(D)\)라 하자. 그러면 \(\int_{\partial \triangle} f(z)dz=0\)이다.
# 증명 ▶
(Proof)
\(D\)에 속하는 임의의 삼각형 \(\triangle\)에 대하여 \(\displaystyle \left|\oint_{\partial \triangle} f(z)dz\right|=0\)임을 보이면 충분하다. 다음 그림과 같이 삼각형 모양의 경로 \(\partial \triangle\)에 대하여 이를 사등분한 \(\partial \triangle_i \; (i=1, 2, 3, 4)\)를 생각하자.
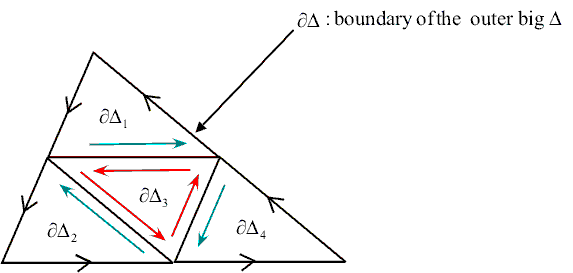
마주보는 삼각형의 변끼리는 경로 적분에서 적분의 방향이 서로 달라 없어지기 때문에 \[\oint_{\partial \triangle} f(z)dz=\oint_{\partial \triangle_1}f(z)dz+\oint_{\partial \triangle_2}f(z)dz+\oint_{\partial \triangle_3}f(z)dz+\oint_{\partial \triangle_4}f(z)dz\]이 성립한다. 따라서 삼각부등식으로부터 \[\left|\oint_{\partial \triangle} f(z)dz\right|\leq \sum_{i=1}^4 \left|\oint_{\partial \triangle_i} f(z)dz\right|\]이 성립하므로 적어도 하나의 \(i=1, 2, 3, 4\)에 대하여 \[\left|\oint_{\partial \triangle_i} f(z)dz\right|\geq \frac{1}{4} \left|\oint_{\partial \triangle} f(z)dz\right|\]이다. 이러한 \(\partial \triangle_i\) 중 하나를 선택하여 \(\partial \triangle ^{(1)}\)이라 하자. \(\partial \triangle^{(1)}\)을 사등분하여 위와 같은 과정으로 얻은 삼각형 모양의 경로를 \(\partial \triangle^{(2)}\)라 하면 \[\left|\oint_{\partial \triangle^{(2)}} f(z)dz\right|\geq \frac{1}{4}\left|\oint_{\partial \triangle^{(1)}} f(z)dz\right|\geq \frac{1}{4^2} \left|\oint_{\partial \triangle} f(z)dz\right|\]이다. 이러한 방법으로 얻은 축소되는 삼각형들의 열 \(\triangle^{(1)}, \; \triangle^{(2)}, \; \cdots, \; \triangle^{(n)}, \; \cdots\)은 다음을 만족시킨다.
(i) \(\triangle \supset \triangle^{(1)}\supset \triangle^{(2)} \supset \cdots \supset \triangle^{(n)}\supset \cdots\)
(ii) \(\displaystyle \left|\oint_{\partial \triangle^{(n)}} f(z)dz\right|\geq \frac{1}{4^n}\left|\oint_{\partial \triangle} f(z)dz\right|\)
(iii) \(\displaystyle \ell\left(\partial \triangle^{(n)}\right)=\frac{1}{2^n}\cdot \ell (\partial \triangle)\)
이제 각 \(n\in \Bbb N\)에 대하여 \(\text{Int}(\triangle^(n)\)의 원소 \(a_n\)을 선택하면 하이네-보렐 정리를 증명할 때와 같은 방법으로 \(\{a_n\}\)은 코시 수열임을 알 수 있다. (또는 2차원에서의 축소 구간 정리를 이용할 수도 있다.) \(\displaystyle \lim_{n\to \infty}a_n=\alpha\)라 하자. \(\alpha\in D\)이고 \(f\)는 \(\alpha\)에서 미분가능하므로 함수 \[g(z)=\begin{cases}\displaystyle \frac{f(z)-f(\alpha)}{z-\alpha}-f'(\alpha) & (z\neq \alpha)\\[.5em]\; 0 & (z=\alpha)\end{cases}\]는 연속이고, 각 \(z\in D\)에 대하여 \[f(z)=f(\alpha)+f'(\alpha)(z-\alpha)+(z-\alpha)g(z)\]이다. 이때 미적분의 기본정리에 의하여 \[\begin{align}&\oint_{\partial\triangle^{(n)}}f(\alpha)dz=\oint_{\partial\triangle^{(n)}}f'(\alpha)(z-\alpha)dz=0 \\[.4em]&\Rightarrow \oint_{\partial\triangle^{(n)}}f(z)dz=\oint_{\partial\triangle^{(n)}}(z-\alpha)g(z)dz \end{align}\]가 성립한다. 이로부터 ML 부등식에 의하여 \[\begin{align} \left|\oint_{\partial\triangle^{(n)}}f(z)dz\right|&\leq\oint_{\partial\triangle^{(n)}}|z-\alpha|\,|g(z)|\,|dz|\\[.4em]&\leq \max_{z\in\partial \triangle^{(n)}}|g(z)|\cdot \max_{z\in \partial\triangle^{(n)}}|z-\alpha|\cdot \frac{1}{2^n}\cdot\ell(\partial \triangle)\\[.4em]&\leq\max_{z\in\partial \triangle^{(n)}}|g(z)|\cdot \frac{\ell(\partial \triangle)^2}{4^n} \\[.3em] & \qquad \qquad (\because \,\forall z\in \partial \triangle^{(n)} \; \Rightarrow |z-\alpha|\leq \ell (\partial \triangle^{(n)}) \end{align}\]이다. 따라서 위의 (iii)에 의하여 \[\frac{1}{4^n}\left|\oint_{\partial\triangle}f(z)dz\right|\leq \left|\oint_{\partial \triangle^{(n)}}f(z)dz\right|\leq \max_{z\in \partial \triangle^{(n)}}|g(z)|\cdot\frac{\ell(\partial \triangle)^2}{4^n}\]이므로 \[\begin{align}\left|\oint_{\partial\triangle}f(z)dz\right|&\leq \max_{z\in \partial \triangle^{(n)}}|g(z)|\cdot\ell(\partial \triangle)^2 \\[.4em]&\leq \max_{|z-\alpha|\leq \text{diam}\left(\triangle^{(n)}\right)}|g(z)|\cdot \ell(\partial\triangle)^2\\[.4em]&=\max_{|z-\alpha|\leq \text{diam}\left(\triangle\right)/2^n} |g(z)|\cdot \ell(\partial\triangle)^2 \end{align}\]이다. 한편, \(g(z)\)는 \(\alpha\)에서 연속이고 \(g(\alpha)=0\)이므로 \(n\to \infty\)일 때 \(\displaystyle \max_{|z-\alpha|\leq \text{diam}\left(\triangle\right)/2^n} |g(z)|\to 0\)이다. 따라서 \(\displaystyle \left|\oint_{\partial\triangle}f(z)dz\right|=0\)이다.
# ◀ 닫기
위 증명이 약간 길지만 이해하기 어렵지는 않을 것이다. 과정을 요약하면 다음과 같다.
(a) 삼각형 모양의 경로를 사등분해서 작은 네 개의 합동인 삼각형을 만들고, 나누어진 삼각형의 적분의 합이 큰 삼각형의 합이 된다는 사실과 삼각부등식을 이용하여 축소되는 삼각형들의 열을 만든다.
(b) (a)에서 만든 삼각형들의 열은 축소되는 삼각형이므로 그 삼각형들 안의 점으로 만든 점열은 한 점으로 수렴한다.
(c) 그 삼각형들의 점열이 수렴하는 점에서의 미분계수를 이용하여 연속함수를 만들고, ML 부등식과 이 연속함수를 이용하여 큰 삼각형의 적분과 작은 삼각형의 적분 사이의 관계식을 만든다.
(d) (c)에서 만든 연속함수의 연속성을 이용하여 큰 삼각형에서의 적분이 \(0\)임을 보인다.
(2)와 (3)은 (1)로부터 비롯되는 자명한 결과이므로 증명이 어렵지 않다.
[Theorem 6.3] (코시의 정리: 볼록도형 모양의 경로)
\(\gamma\)를 볼록한 폐경로(convex contour) \(\gamma^*\)에 의하여 결정되는 조각마다 매끄러운 함수라고 하자. \(D\)를 \(\text{Int}(\gamma)\cup \gamma^*\)를 포함하는 열린 집합이라고 하자. 그러면 \(\displaystyle \int_\gamma f(z)dz=0\)이다.
# 증명 ▶
(Proof)
[Theorem 6.2]에 의하여 \(\partial \triangle \subset \text{Int}(\gamma)\subset D\)인 임의의 삼각형 모양의 폐경로 \(\partial \triangle\)에 대하여 \(\displaystyle \int_{\partial \triangle} f(z)dz=0\)이다. 따라서 \(F\in H(\text{Int}(\gamma))\)이고 \(\forall z\in \text{Int}(\gamma): F'(z)=f(z)\)인 \(F\)가 존재한다. (참고: [Theorem 2.5] - https://greenland.tistory.com/48) 따라서 \(\displaystyle \int_\gamma f(z)dz=\int_\gamma F'(z)dz=0\)이 성립한다.
# ◀ 닫기
(3)의 경우는 다각형을 적절히 여러 개의 삼각형으로 나누어 적분의 합을 구하면 된다. 이때 삼각형의 두 변이 중첩되는 부분에서의 선적분은 방향이 다른 적분이므로 \(0\)이 된다. [Theorem 6.2]에 의하여 삼각형 경로에서의 적분은 \(0\)이 되므로 다각형 모양의 경로 적분도 \(0\)이 된다.

(4)는 다음 보조정리를 이용하여 증명할 수 있다. 증명은 복잡하기 때문에 생략(컴팩트성을 이용한다.)하는데, 미분기하학의 곡선론에서 유한 길이의 곡선을 그 곡선 위의 점들로 이루어진 선분들의 길이의 합으로 나타내어 그 상한으로 정의하는데, 그것과 비슷한 맥락이라고 보면 된다.
[Lemma 6.4] (Approximation Lemma)
\(f\)가 열린 연결집합 \(D\)에서 연속이고 \(\gamma\)를 \(D\) 위의 경로라고 하자. 그러면 임의의 \(\epsilon>0\)에 대하여 꼭짓점이 모두 \(\gamma\) 위에 있는 꺾은선 모양의 경로 \(P\subset D\)가 존재하여 \[\left|\int_\gamma f(z)dz-\int_P f(z)dz\right|<\epsilon\]을 만족시킨다.
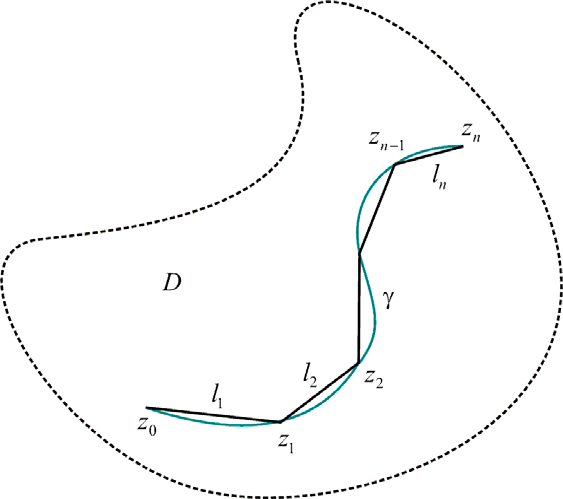
이를 이용하면 (4)의 경우의 증명을 완료할 수 있다.
# 증명 ▶
(Proof of Cauchy's Theorem)
[Lemma 6.4]에 의하여 임의의 \(\epsilon>0\)에 대하여 각 꼭짓점이 \(\gamma\) 위에 있는 꺾은선 모양의 폐경로(polygonal contour) \(P\)가 존재하여 \[\left|\int_\gamma f(z)dz-\int_P f(z)dz\right|<\epsilon\]을 만족시킨다. 이때 [Theorem 6.2]에 의하여 \(\displaystyle \int_P f(z)dz=0\)이므로 \(\displaystyle \left|\int_\gamma f(z)dz\right|<\epsilon\)이다. 이때 \(\epsilon\)은 임의의 양수이므로 \(\displaystyle \left|\int_\gamma f(z)dz\right|=0\)을 얻는다.
# ◀ 닫기
변형 정리(The Deformation Theorem)
코시의 정리의 결과로 나오는 중요한 정리 중 하나가 이 변형 정리이다. 그린 정리에서도 비슷한 정리를 논한 적이 있었는데, 그린 정리의 경우 약간 까다로운 조건(\(Q_x-P_y=0\))을 만족시켜야 하므로 특정한 목적을 가지고 써야 한다. 그러나 복소함수론에서는 조건이 좋은 함수는 경로를 마음껏 변형해도 적분값이 일정하게 된다.
[Theorem 6.5] (변형 정리: The Deformation Theorem)
두 곡선 \(\gamma_1, \; \gamma_2\)가 폐곡선이고 \(\gamma_2\)가 \(\gamma_1\) 안에 완전히 포함되어 있다고 하자. \(\Omega\)가 \(\gamma_1, \; \gamma_2\)로 둘러싸인 부분을 포함하는 열린 집합이라 하고, \(f\in H(\Omega)\)라 하자. 그러면 \[\int_{\gamma_1} f(z)dz=\int_{\gamma_2} f(z)dz\]이다.
# 증명 ▶
(Proof)
\(\gamma_1, \; \gamma_2\)로 둘러싸인 부분을 다음과 같이 선분 \(AB\)와 \(CD\)를 이용하여 나누자.
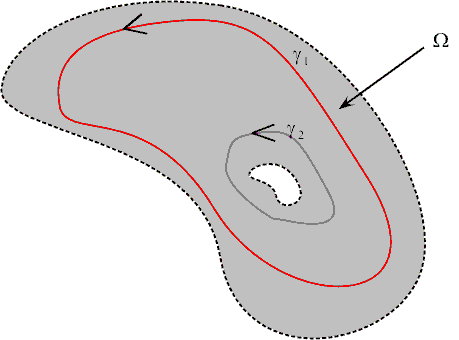
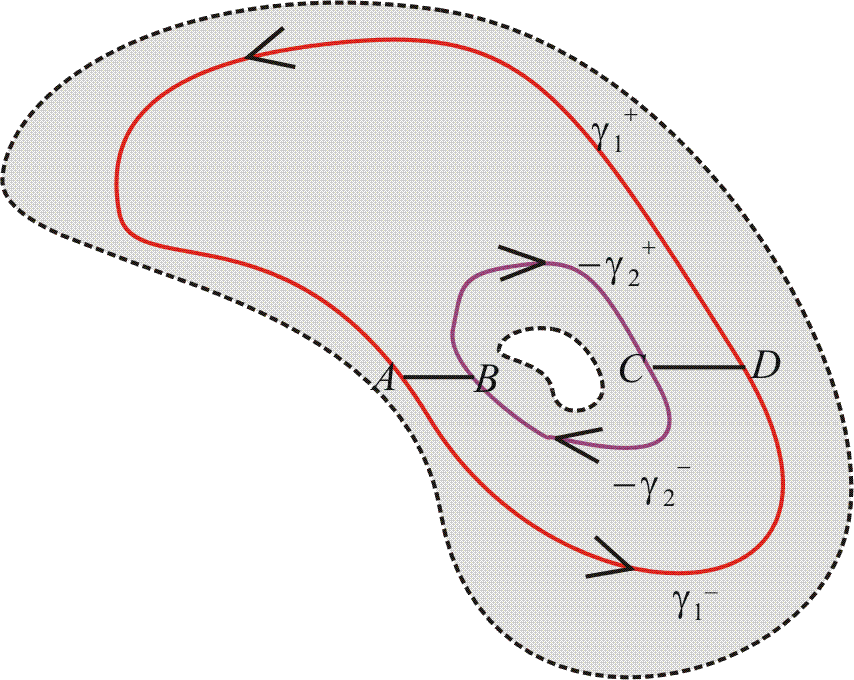
곡선에 \(+, \, -\)를 곡선의 윗부분과 아랫부분을 나타낸다고 하자. 그러면 그림에서 \(AB+(-\gamma_2^+)+CD+\gamma_1^+\)는 폐경로를 이루고 \(f\)는 이 경로와 그 내부에서 정칙(미분가능)이므로 \[\int_{AB+(-\gamma_2^+)+CD+\gamma_1^+}f(z)dz=0\]이다. 따라서 이로부터 다음을 얻는다. \[\int_{\gamma_1^+}f(z)dz=\int_{\gamma_2^+}f(z)dz-\int_{AB}f(z)dz-\int_{CD}f(z)dz \quad \cdots \ (1)\] 비슷한 방법으로 폐경로 \(DC+(-\gamma_2^-)+BA+\gamma_1^-\)로부터 다음을 얻는다. \[\int_{\gamma_1^-}f(z)dz=\int_{\gamma_2^-}f(z)dz-\int_{BA}f(z)dz-\int_{DC}f(z)dz \quad \cdots \ (2)\] 따라서 \(\text{(1)}\)과 \(\text{(2)}\)의 양변을 변변 더하면 \[\color{blue}{\int_{\gamma_1}f(z)dz}\color{black}=\int_{\gamma_1^+}f(z)dz+\int_{\gamma_1^-}f(z)dz=\int_{\gamma_2^+}f(z)dz+\int_{\gamma_2^-}f(z)dz=\color{blue}\int_{\gamma_2}f(z)dz\]
# ◀ 닫기
위의 내용을 확장하면, 다음과 같이 여러 개의 곡선이 있을 때에도 비슷한 정리(일반화된 변형 정리: Extended version of Deformation Theorem)가 성립한다. 가정은 [Theorem 6.5]와 동일하다.

이를 응용한 예시는 다음과 같다.
[Example 6.6]
\(\gamma\)가 \(z_0\)을 포함하는 임의의 폐경로라고 할 때, 충분히 작은 양수 \(r>0\)이 존재하여 \(C_r: |z-z_0|=r\)가 \(\gamma\) 내부에 들어가게 할 수 있다. 따라서 [Theorem 6.5]에 의하여 \[\oint_\gamma (z-z_0)^ndz=\oint_{C_r}(z-z_0)^ndz=\begin{cases}2\pi i & (n=-1)\\[.3em]0 & (n\neq -1)\end{cases}\]가 성립한다.
[Example 6.7]
\(\Gamma\)가 다음과 같은 폐경로일 때, \(\displaystyle \oint_\Gamma \frac{3z-2}{z^2-z}dz\)의 값을 구해 보자.
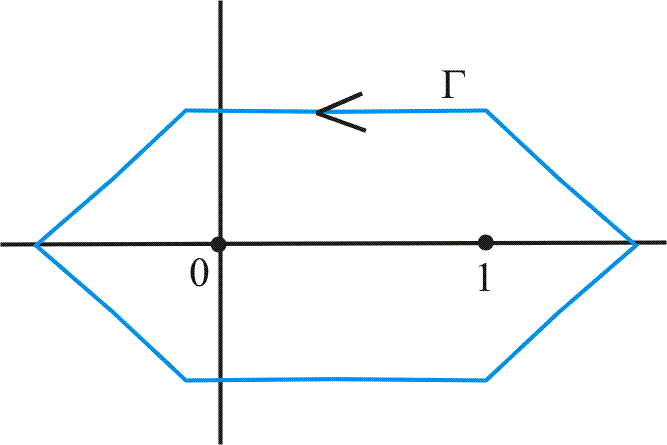
함수 \(\displaystyle \frac{3z-2}{z^2-z}\)는 \(\Bbb C\, \backslash \, \{0, 1\}\)에서 정칙이다. 충분히 작은 \(\epsilon>0\)에 대하여 변형 정리에 의하여 \[\oint_\Gamma \frac{3z-2}{z^2-z}dz=\oint_{|z|=\epsilon}\frac{3z-2}{z^2-z}dz+\oint_{|z-1|=\epsilon}\frac{3z-2}{z^2-z}dz\]가 성립한다. 이때 \(\displaystyle \frac{3z-2}{z^2-z}=\frac{2}{z}+\frac{1}{z-1}\)이다. 이때 \[\oint_{|z|=\epsilon}\frac{3z-2}{z^2-z}dz=\underbrace{\oint_{|z|=\epsilon}\frac{1}{z-1}dz}_{=0\; \text{since} \; \frac{1}{z-1}\in H(N(0,\epsilon))}+\oint_{|z|=\epsilon}\frac{2}{z}dz=4\pi i\]이고, 비슷한 방법으로 \[\oint_{|z-1|=\epsilon}\frac{3z-2}{z^2-z}dz=\oint_{|z-1|=\epsilon}\frac{1}{z-1}dz\underbrace{\oint_{|z-1|=\epsilon}\frac{2}{z}dz}_{=0\; \text{since} \; \frac{2}{z}\in H(N(1,\epsilon))}+=2\pi i\]을 얻을 수 있다. 따라서 \(\displaystyle \oint_\Gamma \frac{3z-2}{z^2-z}dz=6\pi i\)이다.
[Example 6.8]
변형 정리에 의하여 \(a>0,\ b>0\)에 대하여 \(\displaystyle \oint_{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}\frac{1}{z}dz=2\pi i\)이다. 이때 타원 \(\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)의 한 매개변수 표현 \(\gamma(t)=a\cos t+i b \sin t\)를 이용하면 다음을 얻는다. \[\begin{align}2\pi i &=\oint_{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}\frac{1}{z}dz\\[.5em]&=\int_0^{2\pi}\frac{-a\sin t+i b\cos t}{a\cos t+ib\sin t}dt\\[.5em]&=\int_0^{2\pi} \frac{(-a\sin t+ib\cos t)(a\cos t-ib \sin t)}{a^2\cos^2 t+b^2 \sin^2t}dt\\[.5em] &=(b^2-a^2)\int_0^{2\pi}\frac{\sin t\cos t}{a^2\cos^2 t+b^2\sin^2 t}dt+i\int_0^{2\pi}\frac{ab}{a^2\cos^2 t+b^2\sin^2 t}dt \end{align}\] 양변의 허수 부분을 비교하면 \[\int_0^{2\pi} \frac{dt}{a^2\cos^2 t+b^2\sin^2 t}=\frac{2\pi}{ab}\]이다.
Reference: <Complex Analysis> John M. Howie, 2003
'[Undergraduates] > 복소해석학' 카테고리의 다른 글
| [Chapter 7] Some Consequences of Cauchy’s Theorem (0) | 2021.07.08 |
|---|---|
| [Chapter 5] Integration - (3) (0) | 2021.06.02 |
| [Chapter 5] Integration - (2) (0) | 2021.05.18 |