추정(Estimation)
복소함수의 쓰임 중 하나는 특수한 급수나 특이적분의 계산에서의 활용이다. 이때 복소함수의 정적분이 최대 또는 최소가 되는 상황을 이용하는데, 이렇게 어떤 식의 값을 정확히 계산하지 않고, 특정한 목표를 위하여 근삿값을 구하는 것을 추정이라고 한다. 다음은 복소함수의 적분에서 추정을 할 때 가장 기본적으로 쓰이는 부등식이고, 실함수에서의 리만 적분에서와 형태가 동일한 부등식이다.
[Theorem 2.0]
함수 \(f: [a, b] \to \Bbb C\)가 연속이라고 하자. 그러면 다음이 성립한다. \[\left|\int_a^b f(t)dt\right| \leq \int_a^b |f(t)|dt\] [Note] 이는 실함수의 적분에서도 성립한다.
# 증명 ▶
(Proof)
만약 \(\int_a^b f(t)dt=0\)이면 주어진 부등식은 자명히 성립한다. 이제 \(\int_a^b f(t)dt\neq 0\)이라고 하자.
\(\int_a^b f(t)dt\,\)는 복소수이므로 적당한 \(\theta\in \Bbb R\)에 대하여 \[\int_a^b f(t)dt= \left|\int_a^b f(t)dt\right|e^{-i\theta} \ \Rightarrow \ \int_a^b f(t)e^{i\theta}dt=\left|\int_a^b f(t)dt\right|\]가 성립한다. 따라서 복소함수의 적분의 정의와 실함수의 리만적분의 성질에 의하여 \[\begin{align}\left|\int_a^bf(t)e^{it}dt\right|&=\int_a^b f(t)e^{it}dt\\[.4em]&=\int_a^b \text{Re}\left(f(t)e^{it}\right)dt+i\int_a^b \text{Im}\left(f(t)e^{it}\right)dt\\[.4em] &=\int_a^b\text{Re}\left(f(t)e^{it}\right)dt \quad (\because \text{LHS}:\text{Real})\\[.4em]&\leq \int_a^b \left|f(t)e^{it}\right|dt=\int_a^b|f(t)|dt\end{align}\]
# ◀ 닫기
위 정리를 이용하면 복소함수의 정적분의 추정에서 가장 많이 쓰이는 부등식을 얻을 수 있다.
[Theorem 2.1] [ML inequality]
곡선 \(\gamma: [a, b]\to \Bbb C\)가 조각마다 매끄러운 함수라고 하자. 함수 \(f\)가 이 곡선 위의 모든 \(z\)에 대하여 \(|f(z)|\leq M\)을 만족시키는 복소함수라고 하자. 그러면 다음이 성립한다.
(i) \(\displaystyle \left|\int_\gamma f(z)dz\right|\leq M\ell(\gamma)\) (단, \(\ell(\gamma)=\int_a^b |\gamma'(t)|dt\,\)는 곡선 \(\gamma\)의 길이)
특히, \(\left|\int_\gamma f(z)dz\right|\leq \left(\displaystyle \max_{z\in \gamma}|f(z)|\right)\ell(\gamma)\)이 성립한다.
(ii) \(\displaystyle \left|\int_\gamma f(z)dz\right|\leq \int_\gamma |f(z)|dz|\) (Note: \(dz=\gamma'(t)dt\))
# 증명 ▶
(Proof)
(i) \(\displaystyle \int_\gamma f(z)dz=\int_a^b f(\gamma(t))\gamma'(t)dt\,\)이므로 [Theorem 2.0]에 의하여 \[\left|\int_\gamma f(z)dz\right|\leq\int_a^b|f(\gamma(t))||\gamma'(t)|dt\leq M\int_a^b|\gamma'(t)|dt=M\ell(\gamma)\]
(ii) (i)과 비슷한 방법으로 \(|dz|=|\gamma'(t)|dt\)이므로 \[\left|\int_\gamma f(z)dz\right|\leq\int_a^b|f(\gamma(t))||\gamma'(t)|dt\leq \int_\gamma |f(z)||dz|\]
# ◀ 닫기
[Example 2.2]
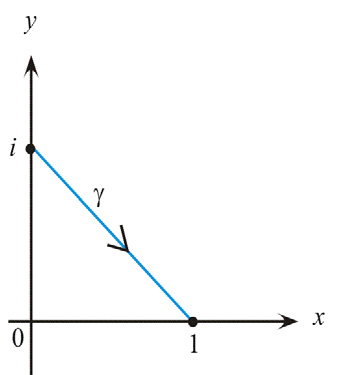
\(\gamma\)가 \(z=i\)과 \(z=1\)을 잇는 선분일 때 \(\displaystyle \left|\int_\gamma \frac{dz}{z^4}\right|\)의 최댓값을 구해 보자. 원점에서 \(\gamma\)까지의 점의 거리의 최솟값은 \(1/\sqrt{2}\)이므로 \(|z|\leq 1/\sqrt{2}\)이다. 따라서 \(\left|\frac{1}{z^4}\right|\leq (\sqrt{2})^4=4\)이므로 [Theorem 2.1]에 의하여 \[\left|\int_\gamma \frac{dz}{z^4}\right|\leq 4\times \ell(\gamma)=4\sqrt{2}\]
[Example 2.3]
함수 \(f(z)=1/(z^3+1)\)라 하고 \(\gamma(t)=Re^{it} \; (0\leq t\leq \pi)\)라 하자. 그러면 \[\begin{align}\left|\int_\gamma f(z)dz\right|&=\left|\int_0^\pi \frac{1}{z^3+1}dz\right|\\[.5em]&=\left|\int_0^\pi \frac{iRe^{it}}{R^3 e^{3it}+1}dt\right|\\[.5em] &\leq \int_0^\pi \frac{R}{|R^3e^{3it}+1|}dt\\[.5em]&\stackrel{\text{if}\; R>1}{\leq}\int_0^\pi \frac{R}{R^3-1}dt=\frac{R\pi}{R^3-1}\end{align}\]이므로 함수의 극한의 대소 관계로부터 \(\displaystyle \lim_{R\to \infty} \left|\int_\gamma f(z)dz\right|=0\)이다.
위의 정리를 이용하여 앞으로 등장하는 여러 정리를 증명할 수 있는데, 우리 교재에서는 이 장에서 위의 정리를 이용하여 부정적분이 존재하기 위한 조건을 제시한다.
[Definition 2.4]
\(\Bbb C\) 위에서의 (폐)경로(contour)란 부분적으로 매끄럽고, 단순 곡선(경로가 중복되지 않는 곡선)이며, 닫힌 곡선(시작점과 끝점이 일치하는 곡선)을 의미한다.
[Theorem 2.5]
\(\gamma\)가 볼록한 경로(임의의 \(a, b\in \Bbb C\)에 대하여 \(a, b\)를 잇는 선분이 항상 \(\text{Int}(\gamma)\) 안에 있는 경로)이고, \(f\)가 \(\text{Int}(\gamma)\cup \gamma^*\)에서 연속이라고 하자. \(\text{Int}(\gamma)\)에 속하는 임의의 삼각형 모양의 경로 \(\partial \triangle\)에 대하여 \(\displaystyle \int_{\partial\triangle} f(z)dz=0\)이면 \(\text{Int}(\gamma)\)에서 정칙인 함수 \(F\)가 존재하여 모든 \(z\in \text{Int}(\gamma)\)에 대하여 \(F'(z)=f(z)\)를 만족시킨다. 즉, \(f\)는 \(\text{Int}(\gamma)\)에서 부정적분을 갖는다.
# 증명 ▶
(Proof)
\(z\in \text{Int}(\gamma)\)라 하자. \(\text{Int}(\gamma)\)는 열린 집합이므로 양수 \(\delta>0\)이 존재하여 \(S(z, \delta)\in \text{Int}(\gamma)\)이다. 따라서 \(|h|<\delta\)인 \(h\in \Bbb C\)를 선택하면 \(z+h\in \text{Int}(\gamma)\)이다. 이때 \(a\in \Bbb C\)를 \(\text{Int}(\gamma)\)의 고정된 한 점이라고 하자. \(\gamma\)는 볼록한 곡선이므로 세 점 \(z, \, z+h, \, a\)를 꼭짓점으로 갖는 삼각형은 \(\text{Int}(\gamma)\) 위에 있다.

두 점 \(a, \,b\)를 잇는 \(a\)에서 \(b\)로의 선분을 \([a, b]\)라 하자. 가정에서 \[\int_{[a, \ z]}f(w)dw+\int_{[z,\ z+h]}f(w)dw-\int_{[a,\ z+h]}f(w)dw=0\]이다. 따라서 \(F(z)=\displaystyle \int_{[a,\ z]}f(w)dw\,\)라 하면 \[\begin{align} F(z+h)-F(z) &=\int_{[a, \ z+h]}f(w)dw-\int_{[a, \ z]}f(w)dw \\[.4em] &=\int_{[z, \ z+h]}f(w)dw \end{align}\]이다. \(f\)가 연속이므로 \(h\to 0\,\)일 때, \[\begin{align}\left|\frac{F(z+h)-F(z)}{h}-f(z)\right|&=\left|\frac{1}{h}\int_{[z, \, z+h]}(f(w)-f(z))dw\right|\\[.4em]&\leq \frac{1}{|h|}\int_{[z, \ z+h]} |f(w)-f(z)|dw\\[.4em]&\leq\frac{1}{|h|}||f(w)-f(z)||_{[z, \, z+h]}\cdot|h| \to 0 \end{align}\]이다. 따라서 도함수의 정의로부터 \(F'(z)=f(z)\)이다.
(Note) \(f(z)=\displaystyle \frac{1}{h}\cdot hf(z)=\frac{1}{h}\int_{[z, \ z+h]}f(z)dw\)
# ◀ 닫기
그린 정리
그린 정리는 미적분학의 기본 정리(FTC)의 2차원 버전이다. 실함수의 적분에서 연속함수의 정적분의 값은 구간의 양 끝점에 의해서만 영향을 받는다. 즉, 연속인 함수는 부정적분 \(F(x)\)를 갖고, \(f: [a, b]\to \Bbb R\)에 대하여 \[\int_a^b f(x)dx=F(b)-F(a)\]가 성립한다. 그린 정리는 어떤 영역에서 정의된 연속함수의 이중적분의 값이 그 경계의 선적분의 값에 의하여 결정된다는 정리이다.
실함수의 FTC에서 닫힌구간 \([a, b]\)이 면적분의 영역의 내부가 되는 것이고, 끝점인 \(a, b\)가 그 영역의 경계라고 생각하면 되겠다. 복소함수 또한 본질은 선적분이므로 그린 정리가 등장한다.
[Theorem 3.0] [Green's Theorem]
곡선 \(C\)가 \(\Bbb R^2\)에서 양의 방향(시계 반대 방향)으로 진행하는 단순 폐곡선이라고 하자. 영역 \(R\)을 \(C\)로 둘러싸인 내부의 영역이라고 하자. 만약 두 함수 \(P(x, y), \, Q(x, y)\)가 \(R\)을 포함하는 열린 집합 \(D\)에서 \(C^1\)급이면 다음이 성립한다. \[\oint_c (Pdx+Qdy)=\iint_R (Q_x-P_y)dxdy\]
그린 정리는 다음과 같은 순서로 일반적인 경우까지 정리를 확장하여 증명한다. (자세한 계산은 생략한다. 직접 해보면 어렵지 않다.)
(Case 1) \(R\)이 다음과 같이 \(y\)축 방향으로 단순한 모양인 경우 (즉, \(R=\{(x,\, y): a\leq x\leq b, \; f_1(x)\leq y\leq f_2(x)\}\)의 형태로 주어진 경우)

\(\displaystyle \oint_\Gamma Pdx=-\iint_R P_y \,dydx\,\)이 성립한다.
(Case 2) \(R\)이 다음과 같이 \(x\)축 방향으로 단순한 모양인 경우 (즉, \(R=\{(x, \, y): c\leq y\leq d, \; g_1(y)\leq x\leq g_2(y)\}\)의 형태로 주어진 경우)

\(\displaystyle \oint_\Gamma Qdy=\iint_R Q_x\, dxdy\,\)이 성립한다.
(Case 1+ Case 2) 다음과 같이 영역 \(R\)이 \(x\)축 방향과 \(y\)축 방향으로 단순한 모양인 경우 (적절히 \(x\)축 또는 \(y\)축과 평행한 직선으로 잘랐을 때, case 1 또는 case 2 모양이 되는 경우)


\(\displaystyle \oint_{\partial R} P(x, y)dx+Q(x, y)dy=\iint_R (Q_x-P_y)dxdy\,\)가 성립한다.
(Case 3) Case 1 또는 Case 2의 형태가 아닌 경우 (곡선의 형태가 단순하지 않은 경우): 적절히 유한개의 단순한 곡선 모양으로 잘라서 계산한다. 이 경우 역시 \(\displaystyle \oint_{\partial R} P(x, y)dx+Q(x, y)dy=\iint_R (Q_x-P_y)dxdy\)가 성립한다.

(Case 4) \(R\)이 단순 연결 공간이 아닌 경우: 영역 바깥의 경계는 시계 반대 방향, 영역 안쪽의 경계는 시계 방향으로의 진행 방향을 갖는다고 하면 \(\int_{\partial R}Pdx+Qdy=\iint_R(Q_x-P_y)dxdy\)가 성립한다.

위 그림에서 \(\partial R=\Gamma_1+\Gamma_2+\Gamma_3\)이고, 위 그림을 다음과 같이 잘라서 (Case 1)~(Case 3)의 내용을 적용하면 된다.

위에서 단순 연결 공간이 아닌 경우에서 경로를 분할하여 적분하는 것은 특수한 경우 내부의 경계의 모양을 다르게 잡아도 정적분의 값이 같다는 것을 알려준다. 즉,
[Theorem 3.1] [Deformation Theorem]
(1) 두 닫힌 곡선 \(\gamma_1,\ \gamma_2\)에 대하여 \(D\)를 \(\gamma_1, \ \gamma_2\)로 둘러싸인 영역을 포함하는 열린 집합이라고 하자. \(P(x, y), \ Q(x, y)\in C^1(D)\,\)이고 \(D\)에서 \(\underline{Q_x-P_y=0}\,\)가 성립하면 \[\int_{\gamma_1}Pdx+Qdy=\int_{\gamma_2} Pdx+Qdy\]이다.
(2) \(\Gamma\)가 닫힌 곡선이고 \(\gamma_1, \, \gamma_2, \, \cdots, \, \gamma_n\,\)이 서로 겹치지 않고 모두 \(\Gamma\) 안에 있다고 하자. \(D\)가 위의 곡선들로 둘러싸인 영역을 포함하는 열린 집합이라고 하자. \(P(x, y), \ Q(x, y)\in C^1(D)\,\)이고 \(D\)에서 \(\underline{Q_x-P_y=0}\,\)가 성립하면 \[\int_\Gamma Pdx+Qdy=\sum_{k=1}^n \int_{\gamma_k}Pdx+Qdy\]
위 정리는 [Theorem 3.0]의 (Case 4)에서 우변이 \(0\)인 경우이다. 다음은 그린 정리를 활용하여 해결하는 여러 문제들의 예이다.
[Example 3.2]
\(\displaystyle \oint_{\frac{x^2}{4}+y^2=1} (2x-y)dx+(x+3y)dy\,\)의 값을 구해 보자. 두 함수 \(2x-y, \; x+3y\)는 \(\Bbb R^2\)에서 \(C^1\)급이고 \(\Bbb R^2\)은 단순 연결 공간이므로 그린 정리에 의하여 \[\begin{align}\oint&=\iint_{\frac{x^2}{4}+y^2\leq 1}(x+3y)_x-(2x-y)_y dxdy\\[.4em]&=\iint_{\frac{x^2}{4}+y^2\leq 1} 2dxdy \\[.4em]&=2\cdot \left(\text{Area of}\ \ \frac{x^2}{4}+y^2\leq1\right)\\[.4em]&=2\cdot 2\pi=4\pi \end{align}\]
[Example 3.3]
원점을 포함하는 임의의 단순 폐곡선 \(C\,\)에 대하여 \(\displaystyle \oint_C \frac{-y}{x^2+y^2}dx+\frac{x}{x^2+y^2}dy\, \)의 값을 구해 보자. \(\displaystyle P=\frac{-y}{x^2+y^2}, \; Q=\frac{x}{x^2+y^2}\)는 \(\Bbb R^2\, \backslash \, \{(0, 0)\}\)에서 \(C^1\,\)급이고 \(Q_x-P_y=0\)이다. 그러나 \(\Bbb R^2\, \backslash\, \{(0, 0)\}\)은 단순 연결 공간이 아니므로 그린 정리를 단순히 적용할 수는 없다.
대신 \(r>0\)을 충분히 작게 잡아서 원 \(x^2+y^2=r^2\)이 곡선 \(C\)의 내부에 들어가게 하면, \(x=r\cos t, \; y=r\sin t\,\)이라 할 때, [Theorem 3.1]에 의하여 \[\begin{align}&\oint_C \frac{-y}{x^2+y^2}dx+\frac{x}{x^2+y^2}dy\\[.4em]&=\oint_{x^2+y^2=r^2}\frac{-y}{x^2+y^2}dx+\frac{x}{x^2+y^2}dy \\[.4em]&=\int_0^{2\pi} \frac{-r\sin t\cdot(-r\sin t)+r\cos t\cdot r\cos t}{r^2}\,dt\\[.4em]&=\int_0^{2\pi}1dt=2\pi \end{align}\]
[Example 3.4]
곡선 \(C\)가 \(\Bbb R^2\)에서 양의 방향으로 진행하는 곡선이고 \(R\)을 \(C\)의 내부라고 하자. 이때 \(\displaystyle \iint_R dxdy\)가 \(R\)의 넓이이므로 그린 정리에 의하여 \[\begin{align}\iint_R dxdy&=\oint_C xdy \quad (\leftarrow P=0, \; Q=x)\\[.4em]&=\oint_C (-y)dx \quad (\leftarrow P=-y, \; Q=0) \\[.4em] &=\frac{1}{2}\oint_C (xdy-ydx)\end{align}\]이 성립한다. 이를 이용하여 성망형(별모양) 곡선 \(x^{2/3}+y^{2/3}=1\) 내부의 넓이를 구하면 다음과 같다. \[\begin{align}\text{Area}&=\frac{1}{2}\oint_{x^{2/3}+y^{2/3}=1}xdy-ydx\\[.4em] \stackrel{x=\cos^3 t, \; y=\sin^3 t}{=}&\ \frac{1}{2}\int_0^{2\pi} (\cos^3 t)(3\sin^2 t \cos t)+(\sin^3 t)(3\cos^2 t\sin t)dt\\[.4em]&=\frac{3}{2}\int_0^{2\pi}\cos^2t \sin^2tdt\\[.4em]&=\frac{3}{8}\int_0^{2\pi} \sin^2{2t}dt=\frac{3\pi}{8} \end{align}\]

[Example 3.5]
\(C=\partial D\)에 대하여 영역 \(D\)는 다음 그림과 같을 때, \(\displaystyle \oint_C y^2dx+3xydy\)의 값을 구해 보자.
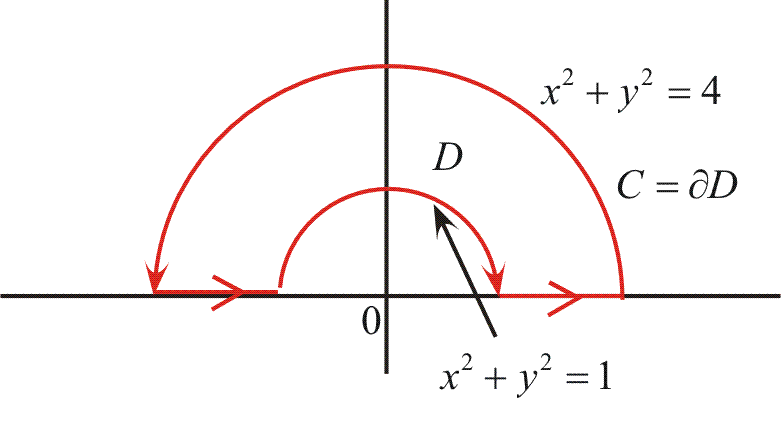
그린 정리와 이중적분의 변수 변환에 의하여 주어진 정적분은 다음과 같다. \[\begin{align}\oint&=\iint_D [(3xy)_x-(y^2)_y\,] dxdy \\[.4em]&=\iint_D y\,dxdy \\[.4em] &=\int_0^\pi \int_1^2 (r\sin\theta)\left|\frac{\partial(x, y)}{\partial(r, \theta)}\right|drd\theta \\[.4em] &=\int_0^\pi \sin\theta d\theta \int_1^2r^2dr=\frac{14}{3}\end{align}\]
Reference: <Complex Analysis> John M. Howie, 2003
'[Undergraduates] > 복소해석학' 카테고리의 다른 글
| [Chapter 5] Integration - (3) (0) | 2021.06.02 |
|---|---|
| [Chapter 5] Integration - (1) (0) | 2021.05.11 |
| [Chapter 4] Differentiation (0) | 2021.04.29 |