[Chapter 9] 가산 공리 (2) - Problems

[Problem 1]

$\mathbb{R}$에서 위상 $\mathcal{T}$를 여유한 위상(cofinite topology)이라 하자.

(1) 위상공간 $(\mathbb{R},\mathcal{T})$가 제1가산공간이 아님을 보여라.
(2) 위상공간 $(\mathbb{R},\mathcal{T})$가 분해 가능 공간(separable space)임을 보여라.

Solution ▶

(Proof)

(1) $(\mathbb{R},\mathcal{T}$\)가 제1가산공간이라고 가정하자. 임의의 $p\in \mathbb{R}$에 대하여 $p$에서의 가산인 국소기저 ${\mathcal{B}}_p=\{B_n\mid n\in \mathbb{N}\}$가 존재한다. 여유한 위상의 정의에 의하여 각 자연수 $n$에 대하여 ${B_n}^c$은 유한집합이다. 따라서 $B=\bigcup _{n=1}^{\mathrm{\infty }}{B_n}^c$은 가산집합이므로 $a\in \mathbb{R}\mathrm{\setminus }B$인 $a\ne p$가 존재하고, $\{a{\}}^c$는 $p$를 포함하는 한 열린 집합이다. 또한 $a\in \mathbb{R}\mathrm{\setminus }B=\bigcap _{n=1}^{\mathrm{\infty }}{B}_n$이므로 모든 자연수 $n$에 대하여 $a\in B_n$이다. 즉, $B_n\not\subset \{a{\}}^c$이다. 이는 ${\mathcal{B}}_p$가 $p$에서의 국소기저라는 사실에 모순이다. 따라서 여유한 위상공간은 제1위상공간이 아니다.

(2) 임의의 $G\in \mathcal{T}$에 대하여 $G^c$는 유한집합이다. $\mathbb{N}$은 무한집합이므로 $G$는 $\mathbb{N}$의 적어도 하나의 원소를 포함한다. 따라서 $\overline{\mathbb{N}}=\mathbb{R}$이다. 

Solution ▶

 

[Problem 2]

분리 가능한 위상 공간의 부분공간이 분리 가능하지 않을 수도 있음을 반례를 들음으로써 증명하여라.

Solution ▶

(Proof)

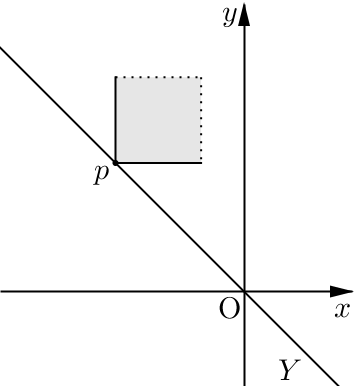
${\mathbb{R}}^2$ 위에서의 위상 $\mathcal{T}$를 반열린 직사각형 $$[a,b)\times [c,d)=\{(x,y)\mid a\le x<b,c\le x<d\}$$에 의하여 생성되는 위상이라고 하자. 이 위상은 분리 가능한 공간이다. ($A=\{[p,q)\times [r,s)\mid p,q,r,s\in \mathbb{Q}\}$라 하면 $\overline{A}={\mathbb{R}}^2$이다.) 이때 집합 $Y$를 $$Y=\{(x,y)\mid x+y=0\}$$라 하면 부분공간 $Y$는 이산 위산공간이다. $Y$는 비가산집합이므로 분리 가능하지 않다.

Solution ▶

 

[Problem 3]

$A$를 제2가산공간 $X$의 비가산인 부분집합이라고 하자. 집합 $A$가 적어도 하나의 집적점을 가지고 있음을 보여라. 

Solution ▶

(Proof)

집합 $A$가 단 하나의 집적점도 가지지 않는다고 하고, $X$의 가산인 기저를 $\mathcal{B}=\{B_n\mid n\in \mathbb{N}\}$라 하자. 그러면 $x_n\in B_n$인 $x_n\in X$에 대하여 $A\cap B_n\subset \{x_n\}$를 만족시킨다. 따라서 $$A=\bigcup \{A\cap B_n\mid n\in \mathbb{N}\}\subset \{x_n\mid n\in \mathbb{N}\}$$이다. 이는 $A$가 비가산집합이라는 데에 모순이다. 따라서 집합 $A$는 적어도 하나의 집적점을 갖는다.

Solution ▶

 

[Problem 4]

$\mathbb{R}$ 위에서의 아래끝 위상 $\mathcal{T}$가 위상공간 $(\mathbb{R},\mathcal{T})$이 분해 가능공간임을 보여라.

Solution ▶

(Proof)

아래끝 위상은 보통 위상보다 큰 위상이다. 따라서 보통 위상에서의 열린 집합은 모두 아래끝 위상에서의 열린 집합이 된다. 보통 위상은 분해 가능 공간이므로 보통 위상에서의 임의의 열린 집합 $G$에 대하여 $\mathbb{Q}\cap G\ne \varnothing$이다. $G$는 아래끝 위상에서의 열린 집합이기도 하므로 $(\mathbb{R},\mathcal{T})$은 분해 가능하다. 

(cf) 실수 $a,b$에 대하여 보통 위상 $\mathcal{U}$의 기저인 원소 $(a,b)$에 대하여 $$(a,b)=\bigcup \{[r,b)\mid r\in \mathbb{Q},r>a\}$$이다. 

Solution ▶

 

[Problem 5]

린델뢰프 공간 $X$의 한 닫힌 부분집합 $A$에 대하여 부분공간 $A$ 또한 린델뢰프 공간임을 보여라.

Solution ▶

(Proof)

$\mathcal{G}=\{G_n\mid n\in \mathbb{N}\}$를 집합 $A$의 가산인 열린 덮개라고 하자. 이때 $A^c$는 열린 집합이고 $X=A\cup A^c$이므로 $\mathcal{G}\cup \{A^c\}$은 $X$의 한 가산인 열린 덮개이다. $X$는 린델뢰프 공간이므로 이 열린 덮개는 유한인 부분덮개 ${\mathcal{G}}^{\ast }$를 갖는다. 따라서 ${\mathcal{G}}^{\ast }\mathrm{\setminus }\{A^c\}$은 $\mathcal{G}$의 유한인 부분덮개이다. 즉, 부분공간 $A$는 린델뢰프 공간이다.

Solution ▶

 

Reference: <SCHAUM'S outlines: General Topology>, Seymour Lipschutz.