컴팩트집합과 컴팩트공간
컴팩트집합은 \(\Bbb R\)에서의 유계인 닫힌구간이 갖는 성질을 일반적인 위상공간의 성질로 확장한 것이다. 이는 해석학에서 하이네-보렐 정리에서 비롯되었다고 할 수 있다. 의미는 대략 무한히 뻗어가지 않는 촘촘한 공간이라고 할 수 있다.
[Theorem 0.0] (Heine-Borel Theorem)
\(\Bbb R\)에서의 닫힌구간 \(I=[a, b]\)에 대하여 \(\{G_i\}\)를 \(I\subset \cup_i\, G_i\)를 만족시키는 열린 집합들의 모임이라고 하자. (즉, \(\{G_i\}\)는 집합 \(A\)의 열린 덮개이다.) 이때 \(\{G_i\}\)의 원소 \(G_{i_1}, \, G_{i_2}, \, \cdots\, G_{i_m}\)가 존재하여 \[I\subset G_{i_1}\cup G_{i_2}\cup \cdots\cup G_{i_m}\]을 만족시킨다.
위의 내용을 일반적인 위상 공간에 적용한 것이 컴팩트집합이다.
[Definition 0.1]
위상공간 \(X\)의 부분집합 \(A\)의 임의의 열린 덮개가 항상 유한인 부분덮개를 가지면 집합 \(A\)를 컴팩트(compact)하다고 한다.
[Example 0.2]
이산 위산공간 \((X, \mathfrak D)\)가 컴팩트할 필요충분조건은 \(X\)가 유한집합인 것이다. 이산 위상공간에서 임의의 홑원소집합은 열린 집합이기 때문이다.
[Example 0.3]
\(\Bbb R\)의 열린구간 \(A=(0, 1)\)은 컴팩트집합이 아니다. \[\mathcal G=\left\{\left(\frac{1}{n+2}, \, \frac{1}{n}\right) \middle | \, n\in \Bbb N\right\}\]이라 하면 이는 \(A\)의 열린 덮개이지만, 이는 유한인 부분덮개를 갖지 않는다. \(\mathcal G\)의 임의의 유한인 부분집합족 \(\mathcal G^*\)에 대하여 \(\mathcal G^*\)의 원소 중 가장 \(0\)에 가까운 하한을 갖는 열린구간 \(\left(1/(n_0+2), 1/n_0\right)\)에 대하여 \(\mathcal G^*\)는 \((0, \, 1/(n_0+2)]\)를 덮지 못하기 때문이다.
컴팩트집합은 여러 가지 성질을 가지고 있는데, 가장 처음으로 컴팩트집합의 연속함수에 의한 상은 컴팩트집합이다. 열린집합의 연속함수의 역상은 열린 집합이기 때문이다.
[Theorem 0.4]
집합 \(X\)에서 \(Y\)로의 연속함수 \(f\)와 컴팩트집합 \(A\subset X\)에 대하여 \(f[A]\) 또한 컴팩트집합이다.
# 증명 ▶
(Proof)
\(\mathcal G=\{G_i\}\)를 \(f[A]\)의 한 열린 덮개라고 하자. 이때 \(\{f^{-1}[G_i]\}\)는 \(A\)의 열린 덮개이고 \(A\)는 컴팩트집합이므로 이 덮개의 유한개의 열린 집합 \(f^{-1}[G_{i_1}], \, f^{-1}[G_{i_2}], \, \cdots, \, f^{-1}[G_{i_m}]\)이 존재하여 \[A\subset f^{-1}[G_{i_1}]\cup f^{-1}[G_{i_2}]\cup \cdots \cup f^{-1}[G_{i_m}]\]을 만족시킨다. 따라서 \[f[A]\subset G_{i_1}\cup G_{i_2}\cup \cdots \cup G_{i_m}\]이다. 즉, \(f[A]\)의 임의의 열린 덮개는 유한인 부분덮개를 갖는다.
# ◀ 닫기
또한, 부분공간의 열린 집합은 원래 공간의 열린 집합과 그 공간을 이용하여 생성하므로 어떤 집합이 부분공간에서 컴팩트한 것과 전체 공간에서 컴팩트한 것은 동치이다. 즉,
[Theorem 0.5]
집합 \(A\)가 위상공간 \((X, \mathcal T)\)의 한 부분집합이라고 하자. 집합 \(A\)가 위상 \(\mathcal T\)에 대하여 컴팩트할 필요충분조건은 \(A\)가 부분공간 \((A, \mathcal T_A)\)에서 컴팩트한 것이다.
[Note] 위 정리가 컴팩트한 집합의 부분집합이 컴팩트하다는 것을 의미하는 것은 아니다. 컴팩트집합 그 자체는 바뀌지 않고, 공간이 바뀌는 것이다. 예를 들어 닫힌구간 \([0, 1]\)은 컴팩트집합이지만 그 부분집합인 \((0, 1)\)은 컴팩트가 아니다.
이런 의미에서 위상공간 \(X\) 그 자체가 컴팩트한 경우, 그 공간을 컴팩트공간이라고 한다.
[Definition 0.6]
위상공간 \(X\)에 대하여 \(X\) 자신이 컴팩트집합인 경우, 이 위상공간을 컴팩트공간(Compact Space)이라고 한다.
위 정리와 함께 컴팩트공간의 부분공간의 여러 성질 중 가장 중요한 것은 다음 두 가지가 있다. 우선 컴팩트집합에서 닫힌 부분집합은 컴팩트집합이다.
[Theorem 0.7]
집합 \(F\)를 컴팩트공간 \(X\)의 닫힌 부분집합이라고 하자. 그러면 \(F\)는 컴팩트집합이다.
# 증명 ▶
(Proof)
\(\mathcal G=\{G_i\}\)를 컴팩트공간 \(X\)의 닫힌 부분집합 \(F\)의 한 열린 덮개라고 하자. 그러면 \(\mathcal G\cup \{F^c\}\)은 \(X\)의 한 열린 덮개이다. \(X\)는 컴팩트이므로 이 덮개는 유한인 부분덮개 \(G^*\)를 갖는다. 이때 \(G^* \, \backslash \, \{F^c\}\)는 \(\mathcal G\)의 유한인 부분덮개이다. 따라서 \(F\)는 컴팩트이다.
# ◀ 닫기
이 다음으로, 유한 교차성이라는 성질을 이용하여 컴팩트집합을 설명하는 방법이 있다.
[Definition 0.8]
집합들의 모임 \(\{A_i\}\)에 속하는 임의의 유한개의 집합 \(A_{i_1}, \, A_{i_2}, \, \cdots, \, A_{i_m}\)이 \[A_{i_1}\cap A_{i_2}\cap \cdots \cap A_{i_m}\neq \varnothing\]을 만족시키면 \(\{A_i\}\)는 유한 교차성(Finite Intersection Property)을 만족한다고 한다.
[Theorem 0.8]
위상공간 \(X\)가 컴팩트공간일 필요충분조건은 유한 교차성을 만족시키는 \(X\)의 임의의 닫힌 부분집합들의 모임 \(\{F_i\}\)가 \(\cap_i\, F_i\neq \varnothing\)을 만족시키는 것이다.
# 증명 ▶
(Proof)
(\(\Rightarrow\)) \(X\)가 컴팩트공간이고 어떤 닫힌 부분집합들의 모임 \(\{F_i\}\)가 유한교차성을 만족시키지만 \(\cap_i \, F_i=\varnothing\)이라 하자. 그러면 \(\cup_i F_i^{\, c}=X\)이므로 \(\mathcal G=\{F_i^{\, c}\}\)는 \(X\)의 한 열린 덮개이다. \(X\)는 컴팩트공간이므로 \(G\)의 유한개의 원소 \(F_{i_1}^{\, c}, \, F_{i_2}^{\, c}, \, \cdots, \, F_{i_m}^{\, c}\)이 존재하여 \(F_{i_1}^{\, c} \cup F_{i_2}^{\, c} \cup \cdots \cup F_{i_m}^{\, c}=X\)을 만족시킨다. 즉, \(F_{i_1}\cap F_{i_2}\cap \cdots \cap F_{i_m}=\varnothing\)이다. 이는 \(\{F_i\}\)가 유한 교차성을 만족시킨다는 데에 모순이다.
(\(\Leftarrow\)) \(X\)가 컴팩트집합이 아니라고 하자. 즉, 어떤 열린 덮개 \(\mathcal G=\{G_i\}\)의 임의의 유한개의 원소 \(G_{i_1}, \, G_{i_2}, \, \cdots, \, G_{i_m}\)이 \(X\)를 덮지 않는다고 하자. 그러면 \({G_i^c}\)은 유한 교차성을 만족시키는 \(X\)의 닫힌 부분집합들의 모임이지만 \(\cap_i G_i^{\, c}=\varnothing\)이다. 주어진 명제의 대우가 참이므로 원래 명제 또한 참이 된다.
# ◀ 닫기
하우스도르프 공간과 컴팩트공간
컴팩트공간과 하우스도르프 공간은 상당한 관련성을 가지고 있다. 첫째로는 하우스도르프 공간이 컴팩트공간이면 정규 공간이 된다는 성질이다. 우선, 일반적으로 위상공간에서 컴팩트집합이 닫힌 집합이 되는 것은 아니지만 (ex. 여유한 위상) 하우스도르프 공간이라면 그 역이 성립한다.
[Theorem 1.0]
하우스도르프 공간의 컴팩트한 부분집합은 닫힌 집합이다.
# 증명 ▶
(Proof)
\(A\)를 하우스도르프 공간 \(X\)의 컴팩트한 부분집합이라고 하자. \(X\)는 하우스도르프 공간이므로 \(A^c\)의 한 점 \(p\)와 \(A\)의 한 점 \(q\)에 대하여 \(p\in G_q\), \(q\in H_q\)인 서로소인 두 열린 집합 \(G_q, \, H_q\)가 각각 존재한다. 이때 \(\mathcal G=\{H_q \mid q\in A\}\)은 \(A\)의 한 열린 덮개이고 \(A\)는 컴팩트집합이므로 \(\mathcal G\)의 유한개의 원소 \(H_{q_1}, \, H_{q_1}, \, \cdots, \, H_{q_m}\)가 존재하여 \(A\subset H_{q_1}\cap H_{q_2}\cap \cdots \cap H_{q_m}\)을 만족시킨다. 이에 대하여 \(p\in G_{i_k}\)이고 \(G_{i_k}\cap H_{i_k}=\varnothing\)이다. \(\cdots \ (*)\)
이제 \[\begin{align} &G=G_{q_1}\cap G_{q_2}\cap \cdots \cap G_{q_m}\, , \\[.4em] &H=H_{q_1}\cup H_{q_2}\cup \cdots \cup H_{q_m}\end{align}\]라 하면 \(G\)는 \(p\in A^c\)을 포함하는 열린 집합(유한 개의 열린 집합의 교집합)이고, \(H\)는 \(A\)를 포함하는 열린 집합이고 \((*)\)에 의하여 \(G\cap H=\varnothing\)이다. 즉 \(p\in G\subset H^c\subset A^c\)이므로 \(p\)는 \(A^c\)의 내점이다. \(p\)는 \(A^c\)의 임의의 한 점이므로 \(A^c\)는 열린 집합이다. 따라서 \(A\)는 닫힌 집합이다.
# ◀ 닫기
위의 정리의 증명 과정을 보면, 컴팩트집합의 열린 덮개는 유한개의 열린 덮개로 축소될 수 있으므로 항상 유한개의 열린 집합의 교집합을 생성할 수 있다는 것에 주목해야 한다. 따라서 위와 같은 방법으로 다음 정리를 유도할 수 있다.
[Theorem 1.1]
두 집합 \(A, \, B\)를 하우스도르프 공간 \(X\)의 두 컴팩트한 부분집합이라고 하자. 이때 \(A\subset G\)이고 \(B\subset H\)인 두 서로소인 열린 집합 \(G, \, H\)가 존재한다.
[Cf] 이를 이용하여 \(X\)가 컴팩트공간이면서 하우스도르프 공간이면 \(X\)가 정규 공간임을 보일 수 있다.
위의 결과를 이용하여 다음과 같은 유용한 정리를 얻어낼 수 있다.
[Theorem 1.2]
컴팩트공간 \(X\)에서 하우스도르프 공간 \(Y\)로의 일대일 연속함수 \(f\)에 대하여 \(X\)와 \(f[X]\)는 위상동형이다.
# 증명 ▶
(Proof)
\(f\)는 \(X\)에서 \(f[X]\)로의 일대일대응이다. \(X\)는 컴팩트공간이므로 \(X\)에서의 닫힌 집합 \(K\)에 대하여 \(K\)는 컴팩트집합이다. 또한 \(f\)는 연속함수이므로 \(f[K]\)는 \(Y\)에서의 컴팩트한 부분집합이다. \(Y\)는 하우스도르프 공간이므로 \(f[K]\)는 \(Y\)에서 닫힌 집합이다. 즉, 함수 \(f\)는 닫힌 함수(closed funtion)이므로 함수 \(f^{-1}\)는 연속이다.
따라서 함수 \(f\)는 \(X\)에서 \(f[X]\)로의 일대일대응이고 쌍연속함수(bicontinuous function)이므로 위상동형사상이다.
# ◀ 닫기
[Example 1.3]
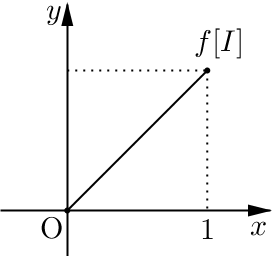
닫힌구간 \(I=[0, 1]\)에서 \(\Bbb R^n\)으로의 일대일 연속함수 \(f\)에 대하여 \(\Bbb R^n\)은 거리 공간이므로 하우스도르프 공간이다. 따라서 [Theorem 1.2]에 의하여 \(I\)와 \(f[I]\)는 위상동형이다. 예를 들어 함수 \[f: [0, 1] \to [0, 1]\times [0, 1], \; \; f(x)=(x, x)\]는 \([0, 1]\)에서 \(\Bbb R^2\)으로의 일대일 연속함수이다. 따라서 \([0, 1]\)과 \(f[I]=\{(x, x)\mid x\in I\}\)은 위상동형이다.
여러 종류의 컴팩트성
일반적으로 정의되는 컴팩트성과 다르게 약한 종류의 컴팩트성을 관찰하고 다룰 수 있다. 이 또한 해석학에서 \(\Bbb R\)의 닫힌 부분집합의 성질을 부분적으로 따온 것이라 할 수 있는데, \(\Bbb R\)과 같은 거리 공간에서는 다음과 같은 여러 컴팩트성이 모두 동치가 된다.
[Definition 2.0]
위상공간 \(X\)의 부분집합 \(A\)에 대하여 집합 \(A\) 위의 임의의 수열이 \(A\)의 한 점으로 수렴하는 부분수열을 가질 때, \(A\)를 점열 컴팩트(Sequentially Compact) 집합이라고 한다.
[Example 2.1]
\(\Bbb R\)에서 열린구간 \(I=(0, 1)\)은 점열 컴팩트가 아니다. \(I\) 위의 수열 \(\{x_n\}\)이 \(x_n=1/n\)일 때, 이 수열은 \(I\) 위에서의 수열이지만 \(I\) 위로 수렴하는 부분수열을 갖지 않는다.
[Definition 2.2]
위상공간 \(X\)의 부분집합 \(A\)에 대하여 \(A\)의 임의의 무한부분집합 \(B\)가 \(A\) 위에서 집적점을 가지면 \(A\)를 극한점 컴팩트(Limit Point Compact)라고 한다.
[Example 2.3]
열린구간 \(I=(0, 1)\)은 극한점 컴팩트가 아니다. [Example 2.1]과 같은 이유이다.
위의 두 컴팩트성은 \(\Bbb R\)의 중요한 성질을 대변하는 다음 정리로부터 유도된 것이라 할 수 있다.
[Theorem 2.4] (Bolzano-Weierstrass Theorem)
유계인 \(\Bbb R\)의 무한 부분집합은 항상 집적점을 갖는다.
우리 책에서는 위 내용을 '가산 컴팩트 공간'이라고 소개하는데, 일반적으로 가산 컴팩트 공간이란 다음을 의미한다.
[Definition 2.5]
위상공간 \(X\)의 가산인 임의의 열린 덮개가 유한인 부분덮개를 갖는 경우 \(X\)를 가산 컴팩트(Countably Compact)라고 한다.
사실 위의 두 공간은 거의 성질이 비슷하다. 위상공간이 \(T_1-\)공간인 경우 두 공간은 서로 같은 공간이 된다.
[Theorem 2.6]
\(X\)가 \(T_1-\)공간이라고 하자. 이때 \(X\)가 가산 컴팩트일 필요충분조건은 \(X\)가 극한점 컴팩트인 것이다.
# 증명 ▶
(Proof)
(\(\Rightarrow\)) \(X\)가 가산 컴팩트이지만 극한점 컴팩트가 아니라고 가정하자. 그러면 \(X\) 위에서 집적점을 갖지 않는 무한 부분집합 \(A\)가 존재한다. 이때 \(A\)를 가산집합이라고 가정해도 무방하다. (비가산인 경우, 가산인 부분집합에 대하여 다음 논의를 진행하면 된다.)
집합 \(A\)는 집적점을 가지지 않으므로 \(X\)의 임의의 원소 \(x\in X\)에 대하여 \(A\cap G_p\subset \{x\}\)인 \(x\)를 포함하는 열린 집합 \(G_x\)가 존재한다. 이때 임의의 \(a\in A\)에 대하여 집합 \(G_{\{a\}}\)와 집합 \(G_{\varnothing}\)를 각각 \[\begin{align} &G_{\{a\}}=\bigcup \{G_x \mid A\cap G_x=\{a\}\}, \\[.4em] &G_{\varnothing}=\bigcup \{G_x \mid A\cap G_x=\varnothing\} \end{align}\]라 하자. 집합 \(A\)는 가산집합이고 각 \(G_x\)는 어떤 \(G_{\{a\}}\)의 부분집합이거나 \(G_{\varnothing}\)의 부분집합이므로 \[\mathcal G=\{G_{\{a\}} \mid a\in A\}\cup \{G_{\varnothing}\}\]은 \(X\)의 가산인 열린 덮개이다. \(X\)는 가산 컴팩트이므로 \(\mathcal G\)는 유한인 열린 부분덮개 \(\mathcal G^*=\{G_1, \, G_2, \, \cdots, \, G_m\}\)을 갖는다. 그러나 \(\mathcal G\)의 구성에서, \(\mathcal G\)의 각 원소는 많아야 \(A\)의 단 한개의 원소만을 가질 수 있으므로 \(\mathcal G\)의 유한개의 원소로는 \(A\)를 덮을 수 없다. 즉, \(G^*\)는 \(X\)의 열린 덮개이지만 \(A\)를 덮을 수 없다. 이는 모순이다.
(\(\Leftarrow\)) \(X\)가 가산 컴팩트가 아니라고 하자. 그러면 유한인 부분덮개를 갖지 않는 가산인 열린덮개 \(\mathcal G=\{G_n \mid n\in \Bbb N\}\)가 존재한다. 즉, \[\begin{align} &a_1\in G_1 \\[.3em] &a_2\in G_2 \, \backslash \, G_1 \\[.3em] &a_3\in G_3 \, \backslash \, (G_1\cup G_2) \\[.3em] & \quad \quad \quad \cdots \\[.3em] &a_n\in G_n\, \backslash \, (G_1\cup G_2\cup \cdots \cup G_{n-1}) \\[.3em] & \quad \quad \quad \cdots \end{align}\]인 각 항이 서로 다른 \(X\) 위의 수열 \(\{a_n\}\)을 구성할 수 있다. 즉, 집합 \(A=\{a_n \mid n\in \Bbb N\}\)는 무한집합이다.
임의의 \(x\in X\)에 대하여 \(\mathcal G\)는 \(X\)의 열린 덮개이므로 \(x\)를 포함하는 \(\mathcal G\)의 원소 \(G_{n_x}\)가 존재한다. \(n_x=m\)이라 하면 집합 \(A\)의 구성에 의하여 \(A\cap G_m \subset \{a_1, \, a_2, \, \cdots, \, a_{m-1}\}\)이다. \(X\)는 \(T_1-\)공간이므로 \(\{a_1, \, a_2, \, \cdots, \, a_{m-1}\}\)은 닫힌 집합이다. 따라서 \(G_m\cap \{a_1, \, a_2, \, \cdots, \, a_{m-1}\}^c\)은 열린 집합이고 \[A\cap (G_m \cap \{a_1, \, a_2, \, \cdots, \, a_{m-1}\}^c)=\varnothing\]이다. 따라서 \(A\)는 \(X\) 위에서 집적점을 갖지 않는다.
# ◀ 닫기
일반적으로 극한점 컴팩트는 가장 약한 조건이다. [Theorem 2.6]에서 가산 컴팩트 공간은 극한점 컴팩트 공간임을 알 수 있다. 위상공간이 \(T_1-\)공간일 때에는 역도 성립하는 것이다. 위의 정리와 함께 다음 또한 성립한다.
[Theorem 2.7]
위상공간 \(X\)가 컴팩트공간이면 \(X\)는 극한점 컴팩트 공간이다.
# 증명 ▶
(Proof)
위상공간 \(X\)가 극한점 컴팩트공간이 아니라고 가정하자. 그러면 \(X\) 위에서 집적점을 갖지 않는 무한 부분집합 \(A\)가 존재한다. 따라서 임의의 \(x\in X\)에 대하여 \(x\)의 열린 근방 \(G_x\)가 존재하여 \(A\cap G_x\subset \{x\}\)를 만족시킨다. 이때 \(\mathcal G=\{G_x \mid x\in X\}\)는 \(X\)의 열린 덮개이다. 각 \(x\in X\)에 대하여 \(A\cap G_x\)는 많아야 한 개의 원소를 가지므로 \(\mathcal G^*\)의 유한개의 원소로는 \(A\)를 덮을 수 없다. 따라서 \(\mathcal G\)는 유한개의 부분덮개를 가질 수 없다. 따라서 \(X\)는 컴팩트공간이 아니다.
# ◀ 닫기
[Theorem 2.8]
위상공간 \(X\)가 점열 컴팩트 공간이면 \(X\)는 극한점 컴팩트 공간이다.
# 증명 ▶
(Proof)
\(X\)가 점열 컴팩트 공간이라 하고, \(A\)를 \(X\) 위의 무한 부분집합이라고 하자. 이때 \(A\)를 가산집합이라고 가정해도 무방하다. \(A=\{a_n \mid n\in \Bbb N\}\)이라 하면 수열 \(\{a_n\}\)은 \(X\) 위의 수열이므로 \(X\) 위의 한 점 \(p\)로 수렴한다. 즉, \(p\)를 포함하는 임의의 열린 집합은 \(A\)의 무수히 많은 원소를 포함한다. 따라서 \(X\)는 극한점 컴팩트 공간이다.
[Cf] 위상공간 \(X\)의 부분집합 \(A\)의 집적점을 \(p\)라 하자. \(p\)를 포함하는 임의의 열린 집합이 \(A\)의 무수히 많은 원소를 포함하는 경우, \(p\)를 \(\omega-\)집적점(\(\omega-\)Accumulation Point)라고 한다.
# ◀ 닫기
Reference: <SCHAUM'S outlines: General Topology>, Seymour Lipschutz.
'[Undergraduates] > 위상수학' 카테고리의 다른 글
| [Chapter 11] 컴팩트성 - (2) (2) | 2021.04.27 |
|---|---|
| [Chapter 10] 분리 공리 (2) - Problems (0) | 2021.04.10 |
| [Chapter 10] 분리 공리 (1) (0) | 2021.04.07 |