코시의 정리
코시의 정리 또는 코시-구르사(Cauchy-Goursat)의 정리라 불리는 정리는 복소해석학의 가장 중심적이고 핵심적인 정리 중 하나이다. 이로부터 코시의 적분 공식, 리우빌 정리, 해석함수의 성질 등 여러 가지를 유도할 수 있다. 얼핏 보면 미적분의 기본 정리와 비슷해 보이지만, 본질적으로 피적분함수의 도함수의 연속성을 가정하지 않는다는 점에서 다르다. 우선 코시의 정리의 진술은 다음과 같다.
[Theorem 6.0] [The Cauchy-Goursat Theorem: 코시-구르사의 정리]
처음 코시는 이 정리에 대한 증명을 더 강한 전제 조건 아래에서 제시하였다. 즉,
[Theorem 6.1]
증명 ▶
(Proof)
(Note) 위의 증명에서
구르사는 [Theorem 6.0]과 같이
(1) 삼각형 모양의 경로
(2) 볼록도형
(3) 다각형(볼록성과 관계 없는)
(4) 일반적인 조각마다 매끄러운 곡선
사실 구르사가 증명한 (1)의 내용이 이 코시의 정리에서 가장 중요하다고 할 수 있다. 나머지는 모두 (1)을 이용한 응용과 그 결과라고 할 수 있기 때문이다.
[Theorem 6.2] (코시의 정리: 삼각형 모양의 경로)
증명 ▶
(Proof)

마주보는 삼각형의 변끼리는 경로 적분에서 적분의 방향이 서로 달라 없어지기 때문에
(i)
(ii)
(iii)
이제 각
위 증명이 약간 길지만 이해하기 어렵지는 않을 것이다. 과정을 요약하면 다음과 같다.
(a) 삼각형 모양의 경로를 사등분해서 작은 네 개의 합동인 삼각형을 만들고, 나누어진 삼각형의 적분의 합이 큰 삼각형의 합이 된다는 사실과 삼각부등식을 이용하여 축소되는 삼각형들의 열을 만든다.
(b) (a)에서 만든 삼각형들의 열은 축소되는 삼각형이므로 그 삼각형들 안의 점으로 만든 점열은 한 점으로 수렴한다.
(c) 그 삼각형들의 점열이 수렴하는 점에서의 미분계수를 이용하여 연속함수를 만들고, ML 부등식과 이 연속함수를 이용하여 큰 삼각형의 적분과 작은 삼각형의 적분 사이의 관계식을 만든다.
(d) (c)에서 만든 연속함수의 연속성을 이용하여 큰 삼각형에서의 적분이
(2)와 (3)은 (1)로부터 비롯되는 자명한 결과이므로 증명이 어렵지 않다.
[Theorem 6.3] (코시의 정리: 볼록도형 모양의 경로)
증명 ▶
(Proof)
[Theorem 6.2]에 의하여
(3)의 경우는 다각형을 적절히 여러 개의 삼각형으로 나누어 적분의 합을 구하면 된다. 이때 삼각형의 두 변이 중첩되는 부분에서의 선적분은 방향이 다른 적분이므로

(4)는 다음 보조정리를 이용하여 증명할 수 있다. 증명은 복잡하기 때문에 생략(컴팩트성을 이용한다.)하는데, 미분기하학의 곡선론에서 유한 길이의 곡선을 그 곡선 위의 점들로 이루어진 선분들의 길이의 합으로 나타내어 그 상한으로 정의하는데, 그것과 비슷한 맥락이라고 보면 된다.
[Lemma 6.4] (Approximation Lemma)

이를 이용하면 (4)의 경우의 증명을 완료할 수 있다.
증명 ▶
(Proof of Cauchy's Theorem)
[Lemma 6.4]에 의하여 임의의
변형 정리(The Deformation Theorem)
코시의 정리의 결과로 나오는 중요한 정리 중 하나가 이 변형 정리이다. 그린 정리에서도 비슷한 정리를 논한 적이 있었는데, 그린 정리의 경우 약간 까다로운 조건(
[Theorem 6.5] (변형 정리: The Deformation Theorem)
두 곡선
증명 ▶
(Proof)
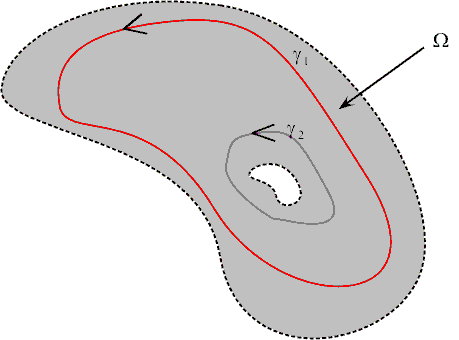
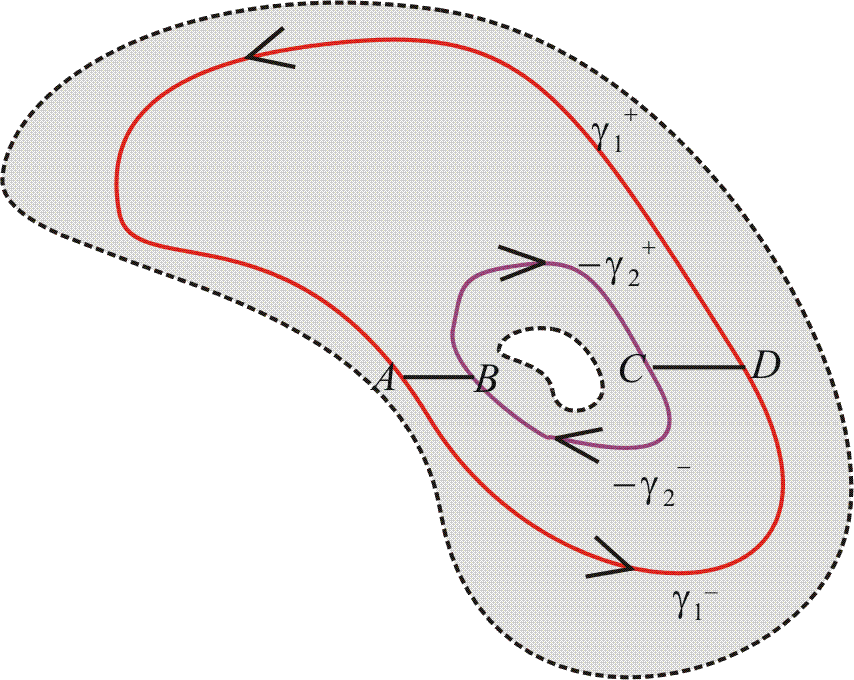
곡선에
위의 내용을 확장하면, 다음과 같이 여러 개의 곡선이 있을 때에도 비슷한 정리(일반화된 변형 정리: Extended version of Deformation Theorem)가 성립한다. 가정은 [Theorem 6.5]와 동일하다.

이를 응용한 예시는 다음과 같다.
[Example 6.6]
[Example 6.7]

함수
[Example 6.8]
변형 정리에 의하여
Reference: <Complex Analysis> John M. Howie, 2003
'[Undergraduates] > 복소해석학' 카테고리의 다른 글
| [Chapter 7] Some Consequences of Cauchy’s Theorem (0) | 2021.07.08 |
|---|---|
| [Chapter 5] Integration - (3) (0) | 2021.06.02 |
| [Chapter 5] Integration - (2) (0) | 2021.05.18 |