제1기본형식
공간의 임의의 곡선은 곡률과 열률이라는 두 가지 불변량에 의하여 정확히 하나로 결정된다. 곡면도 그와 같이 두 가지 불변량인 '제1기본형식'과 '제2기본형식'에 의하여 유일하게 결정된다.
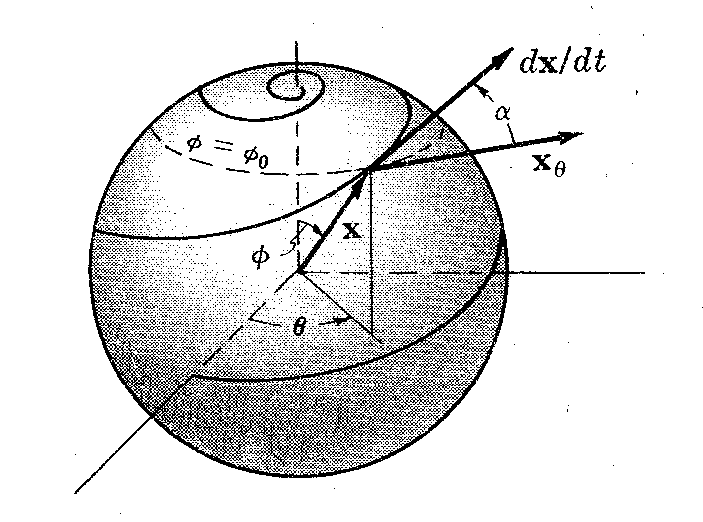
곡면의 적당한 좌표 조각 \(\mathbf x=\mathbf x(u, v)\)에 대하여 \(uv\)평면 위의 한 점 \((u, v)\)에 대하여 이 점에서의 미분(differential) \(d\mathbf x\)는 \(uv\)평면 위의 점 \((u, v)\)에서의 진행 방향의 (미소)벡터 \((du, dv)\) (이때 \(uv\)평면에서 점 \((u, v)\)가 어떤 경로를 따라 이동한다고 생각하면 된다.)에 대하여 \[d\mathbf x=\mathbf x_udu+\mathbf x_vdv\]로 정의되는 벡터이다.
또한, 다변수함수에서의 테일러 정리에 의하여 \[\mathbf x(u+du, v+dv)=\mathbf x(u, v)+d\mathbf x+\mathbf o((du^2+dv^2)^{1/2})\]가 성립한다. 즉, \(d\mathbf x\)는 곡면 위의 점 \(\mathbf x(u, v)\)에서 벡터 \(\mathbf x(u+du, v+dv)-\mathbf x(u, v)\)의 일차 근사이고, 이 점에서의 접평면 위에서 \((u, v)\)의 진행방향으로의 벡터이다. 이를 그림으로 나타내면 다음과 같다.

이때 미분 \(d\mathbf x\)를 이용하여 \[\begin{align}\mathrm I&=|d\mathbf x|^2=d\mathbf x\cdot d\mathbf x \\[.4em] &=(\mathbf x_udu+\mathbf x_vdv)\cdot (\mathbf x_udu+\mathbf x_vdv)\\[.4em] &=(\mathbf x_u\cdot\mathbf x_u)du^2+2(\mathbf x_u\cdot \mathbf x_v)dudv+(\mathbf x_v\cdot \mathbf x_v)dv^2\end{align}\]으로 정의되는 함수 \(\mathrm I\)를 제1기본형식이라고 한다.
[Definition 9.0] [제1기본형식: The First Fundamental Form]
곡면의 \(C^1\)급 이상의 좌표 조각 \(\mathbf x=\mathbf x(u, v)\)에 대하여 \[\begin{align}\mathbf I=\, & Edu^2+2Fdudv+Gdv^2\\[.4em] &(E=\mathbf x_u\cdot \mathbf x_u\, , \; F=\mathbf x_u\cdot \mathbf x_v\, , \; G=\mathbf x_v\cdot \mathbf x_v)\end{align}\]를 \(\mathbf x=\mathbf x(u, v)\)의 제1기본형식(first fundamental form)이라고 하고, 위의 각 계수 \(E\), \(F\), \(G\)를 제1기본계수(first fundamental coefficients)라고 한다.
기본적으로 제1기본형식의 계수 \(E\), \(F\), \(G\)는 \(u, \, v\)의 값에 의존하긴 하지만, 매개변수 \(u, \, v\)의 값이 고정된 경우(즉, 곡면 위의 고정된 한 점에 대하여) \(du, \, dv\)에 의하여 정해진다. 다시 말해서 제1기본형식은 매개변수 평면의 점 \((u, v)\)의 이동 방향에 의존하는 함수이다. \[ \Rightarrow \; \mathrm I=\mathrm I(du, dv)=Edu^2+2Fdudv+Gdv^2\] 한편, 위의 논의는 제1기본형식이 곡면 그 자체의 성질이라는 것을 말해주기도 한다. 왜냐하면 제1기본형식은 어떤 곡면 위의 점에서 그 근방으로의 벡터에 의존하는 개념이기 때문이다. (곡면이 있으면, 그 곡면을 어떻게 표현하든 접평면은 동일할 것이다.)
\(\mathbf x=\mathbf x^*(\theta, \phi)\)를 \(\mathbf x=\mathbf x(u, v)\)의 근방에서 정의된 다른 좌표 조각이라고 하자. 그러면 \((u, v)\)에서 \((\theta, \phi)\)로의 매개변수 변환 \(\theta=\theta(u, v)\), \(\phi=\phi(u, v)\)가 존재하여 \[d\theta=\theta_u du+\theta_v dv\, , \ \ d\phi=\phi_u du+\phi_v dv\]를 만족시킨다. 따라서 두 매개변수 표현 \(\mathbf x\), \(\mathbf x^*\)의 제1기본형식 \(\mathrm I\), \(\mathrm I^*\)에 대하여 \[\begin{align}\mathrm I^*(d\theta, d\phi)&=|d\mathbf x^*|^2=\left|(\mathbf x^*_\theta d\theta+ \mathbf x^*_\phi d\phi)\right|^2\\[.4em]&=\left|\mathbf x_\theta^*(\theta_udu+\theta_vdv)+\mathbf x_\phi^*(\phi_udu+\phi_vdv)\right|^2\\[.4em]&=\left|(\mathbf x_\theta^*\theta_u+\mathbf x_\phi^*\phi_u)du+(\mathbf x_\theta^*\theta_v+\mathbf x_\phi^*\phi_v)dv\right|^2\\[.4em] &=\left|\mathbf x_udu+\mathbf x_vdv\right|^2=|d\mathbf x|^2=\mathrm I(du, dv) \end{align}\]이 성립한다. 즉, 제1기본형식은 매개변수의 표현(좌표 조각의 종류)에 영향을 받지 않는다. 다만, 일차 기본 계수는 당연히 좌표 조각에 영향을 받는다. 계산을 통해 위의 \(\mathbf x=\mathbf x^*(\theta, \phi)\)와 그 일차 기본계수 \(E^*\), \(F^*\), \(G^*\)에 대하여 \[\begin{align}&E=E^*\theta_u^{\,2}+2F^*\theta_u\phi_u+G^*\phi_u^{\, 2}\\[.4em]&F=E^*\theta_u\theta_v+F^*(\theta_u\phi_v+\theta_v\phi_u)+G^*\phi_u\phi_v\\[.4em]&G=E^*\theta_v^{\,2}+2F^*\theta_v\phi_v+G^*\phi_v^{\, 2} \end{align}\]이다. 마지막으로 \(\mathrm I=|d\mathbf x|^2\)이므로 일차기본형식은 항상 양의 부호를 갖는다. 일차기본형식을 \(du, dv\)에 대한 이차식으로 본다면, 이차식과 판별식의 성질로부터 \(E>0, \ G>0, \ EG-F^2>0\)이어야 한다. 실제로 \[\begin{align}EG-F^2&=|\mathbf x_u|^2|\mathbf x_v|^2-(\mathbf x_u\cdot \mathbf x_v)^2\\[.4em] &=|\mathbf x_u|^2|\mathbf x_v|^2(1-\cos^2\alpha)\\[.4em] &=(|\mathbf x_u||\mathbf x_v|\sin\alpha)^2=|\mathbf x_u\times \mathbf x_v|^2 \end{align}\] (단, \(\alpha\)는 두 벡터 \(\mathbf x_u, \, \mathbf x_v\)가 이루는 각이다.)이고, 정칙 매개변수 표현에서 \(\mathbf x_u\times \mathbf x_v\neq 0\)가 성립한다.
[Example 9.1]
곡면 \(\mathbf x=(u+v, \ u-v, \ uv)\)에 대하여 \(\mathbf x_u=(1, 1, v)\), \(\mathbf x_v=(1, -1, u)\)이므로 \(E=\mathbf x_u\cdot \mathbf x_u=2+v^2\), \(F=\mathbf x_u\cdot \mathbf x_v=uv\), \(G=\mathbf x_v\cdot \mathbf x_v=2+u^2\)이다. 따라서 \[\mathrm I=(2+v^2)du^2+2uv\,dudv+(2+u^2)dv^2\]이다. 또한, 모든 \((u, v)\)에 대하여 \(E>0\), \(G>0\), \(EG-F^2=4+2u^2+2v^2>0\)임을 확인할 수 있다. 이때 \(\theta=u+v\), \(\phi=u-v\)인 매개변수 변환을 통해 \[\mathbf x=(\theta, \ \phi, \ \frac{1}{4}(\theta^2-\phi^2))\]을 얻을 수 있다. 이를 이용하여 \[E^*=1+\frac{1}{4}\theta^2, \ \ F^*=-\frac{1}{4}\theta\phi\, , \ \ G^*=1+\frac{1}{4}\phi^2\]을 얻는다. \(u=1, \ v=1\)일 때 \(E=3, \; F=1, \; G=3\)이지만 이에 대응하는 \(\theta=2, \; \phi=0\)에 대하여 \(E^*=2, \; F^*=0, \; G=1\)이므로 제1기본계수는 매개변수 표현에 따라 변할 수 있다.
한편, 제1기본형식을 이용하면 곡면 위의 곡선의 길이와 매개변수 평면의 특정 영역에서 정의된 곡면의 넓이를 구할 수 있다.
곡면 위의 곡선은 곡면의 좌표 조각 \(\mathbf x=\mathbf x(u, v)\)에 대하여 매개변수 평면에서 매개화된 특정 곡선 \((u(t), v(t)) \; (a\leq t\leq b)\)을 따라 움직이는 점 \((u, v)\)에 대한 상 \(\mathbf x=\mathbf x(u(t), \,v(t)) \; (a\leq t\leq b)\)이다. 이는 좌표 조각의 성질에 의하여 정칙 곡선이 되고, 곡선의 길이 공식에 따라 \[\begin{align} s&=\int_a^b \left|\frac{d\mathbf x}{dt}\right|dt=\int_a^b\sqrt{\frac{d\mathbf x}{dt}\cdot \frac{d\mathbf x}{dt}}\, dt\\[.5em] &=\int_a^b\sqrt{\left(\mathbf x_u\frac{du}{dt}+\mathbf x_v\frac{dv}{dt}\right)\cdot \left(\mathbf x_u\frac{du}{dt}+\mathbf x_v\frac{dv}{dt}\right)}\, dt\\[.5em]&=\int_a^b\sqrt{E\left(\frac{du}{dt}\right)^2+2F\frac{du}{dt}\frac{dv}{dt}+G\left(\frac{dv}{dt}\right)^2}dt=\int_a^b \sqrt{\mathrm I\, }\, dt \end{align}\]이다. 따라서
[Theorem 9.2]
곡면의 좌표 조각 \(\mathbf x=\mathbf x(u, v)\)에 대하여 매개변수 평면 위에서의 정칙 곡선 \(\gamma(t)=(u(t), \, v(t)) \; (a\leq t\leq b)\)에 대하여 그 곡선의 곡면 위로의 상인 \(\mathbf x=\mathbf x(u(t), \, v(t))\)의 길이는 \[s=\int_a^b \sqrt{\mathrm I\,}\, dt=\int_a^b \sqrt{E\left(\frac{du}{dt}\right)^2+2F\frac{du}{dt}\frac{dv}{dt}+G\left(\frac{dv}{dt}\right)^2}dt\]
다시 한 번 제1기본형식은 기본적으로 매개변수 평면 위의 한 점에서 점 \((u, v)\)의 이동 방향에 의존하는 함수임을 상기하자. 매개변수 평면의 한 점 \((u, v)\)가 정해진 경우, 그 점이 이동하는 방향이 정해지면 그 점에 해당하는 곡면 위의 점의 이동 방향도 결정된다.
\(uv\)평면 위의 한 점 \((u, v)\)에 대하여 그 점에서의 이동 방향을 나타내는 두 벡터 \((du,\, dv)\)와 \((\delta u,\, \delta v)\)에 대하여 (실제로 계산할 때에는 \((du, dv)\)와 \((\delta u, \delta v)\)를 나타내는 적절한 매개변수 평면 위의 곡선으로 나타내어진다.) 두 미분 \[d\mathbf x=\mathbf x_udu+\mathbf x_v dv, \ \ \delta \mathbf x=\mathbf x_u \delta u+\mathbf x_v \delta v\]이 이루는 각 \(\alpha\)에 대하여 (미분이란 곡면 위의 점에서의 접평면 위의 진행 방향으로의 접벡터이다.) \[\begin{align}\cos\alpha &=\frac{d\mathbf x\cdot \delta\mathbf x}{|d\mathbf x||\delta\mathbf x|
}=\frac{(\mathbf x_udu+\mathbf x_vdv)\cdot(\mathbf x_u\delta u+\mathbf x_v \delta v)}{|\mathbf x_udu+\mathbf x_vdv||\mathbf x_u\delta u+\mathbf x_v \delta v|}\\[.5em]&=\frac{Edu\delta u+F(du\delta v+dv\delta u)+Gdv\delta v}{\sqrt{Edu^2+2Fdudv+Gdv^2}\; \sqrt{E\delta u^2+2F\delta u\delta v+G\delta v^2}}\end{align}\]이다. 특히, \(u-\)매개변수 곡선과 \(v-\)매개변수 곡선이 \((u, v)\)에 대응되는 곡면 위의 점에서 이루는 각(즉, 두 매개변수에 접하는 벡터들이 이루는 각)을 \(\beta\)라 하면 \[\cos\beta=\frac{\mathbf x_u\cdot \mathbf x_v}{|\mathbf x_u||\mathbf x_v|}=\frac{\mathbf x_u\cdot \mathbf x_v}{\sqrt{\mathbf x_u\cdot \mathbf x_u}\ \sqrt{\mathbf x_v\cdot \mathbf x_v}}=\frac{F}{\sqrt{EG}}\]을 얻는다. 이로써 다음 정리를 얻을 수 있다.
[Theorem 9.3]
(1) 두 미분(접벡터) \(d\mathbf x=\mathbf x_udu+\mathbf x_v dv, \; \delta \mathbf x=\mathbf x_u \delta u+\mathbf x_v \delta v\)가 곡면 위의 한 점에서 수직일 필요충분조건은 \[\cos\alpha=0 \ \Leftrightarrow \ E\, du\delta u+F(du\delta v+dv\delta u)+G dv\delta v=0\]인 것이다.
(2) \(u-\)매개변수 곡선과 \(v-\)매개변수 곡선이 곡면 위의 어떤 점에서 수직일 필요충분조건은 \(F=0\)인 것이다.
[Example 9.4]
좌표공간의 단위 구 \(\mathbf x=(\cos\theta\sin\phi, \, \sin\theta\sin\phi, \, \cos\phi)\)와 매개변수 평면 \(\theta\phi-\)평면 위의 곡선 \[\theta=\log\cot(\pi/4-t/2), \ \ \phi=\pi/2-t \ \ (0\leq t\leq \pi/2)\]의 상(구 위의 곡선)을 생각하자. 이때 \[\begin{align}&\mathbf x_\theta=(-\sin\theta\sin\phi, \, \cos\theta\sin\phi, \, 0)\\[.4em] &\mathbf x_\phi=(\cos\theta\cos\phi, \, \sin\theta\cos\phi,\, -\sin\phi) \\[.4em] &\Rightarrow \, E=\mathbf x_\theta\cdot \mathbf x_\theta=\sin^2\phi, \;F=\mathbf x_\theta\cdot \mathbf x_\phi=0, \; G=\mathbf x_\phi\cdot \mathbf x_\phi=1 \\[.4em] &\frac{d\theta}{dt}=\frac{\csc^2(\pi/4-t/2)}{2\cot(\pi/4-t/2)}=\frac{1}{\sin(\pi/2-t)}=\sec t, \ \ \frac{d\phi}{dt}=-1\end{align}\]이다. 따라서 이 곡선의 진행 방향을 따라 계산되는 제1기본형식은 \[\begin{align}\mathrm I&=E\left(\frac{d\theta}{dt}\right)^2+2F\frac{d\theta}{dt}\frac{d\phi}{dt}+G\left(\frac{d\phi}{dt}\right)^2\\[.4em]&=\sin^2\phi \sec^2t+1\\[.4em]&=\sin^2\left(\pi/2-t\right)\sec^2t+1=2\end{align}\]이다. 이로부터 \(0\leq t\leq \pi/2\)에서 곡선의 길이 \(s\)는 \[s=\int_0^{\pi/2}\sqrt{\mathrm I}\,dt=\int_0^{\pi/2}\sqrt{2}\, dt=\frac{\pi}{\sqrt{2}}\]이다. 또한, 이 곡선과 \(\theta-\)매개변수 곡선은 일정한 각을 이루는데, 그 두 각의 크기를 \(\alpha\)라 하면 \[\begin{align}\cos\alpha&=\cos\angle\left(\frac{d\mathbf x}{dt}, \, \mathbf x_\theta\right)=\frac{\left(\mathbf x_\theta\frac{d\theta}{dt}+\mathbf x_\phi\frac{d\phi}{dt}\right)\cdot \mathbf x_\theta}{\left|\mathbf x_\theta\frac{d\theta}{dt}+\mathbf x_\phi\frac{d\phi}{dt}\right||\mathbf x_\theta|}\\[.4em]&=\frac{E\frac{d\theta}{dt}+F\frac{d\theta}{dt}}{\sqrt{\mathrm I\,}\sqrt{E\,}}=(\sin^2\phi\sec t)\cdot\frac{1}{\sqrt{2}\sin\phi}=\frac{1}{\sqrt 2}\end{align}\]이므로 \(\alpha=\pi/4\)이다.
한편, 다음과 같이 곡면 위의 한 점 \(\mathbf x(u, v)\)의 근방에서 \(u-\)매개변수 곡선과 \(v-\)매개변수 곡선들로 둘러싸인 작은 영역 \(\Delta R\)의 넓이는 그 영역이 충분히 작다면 \(\Delta \mathbf x_1= \mathbf x_u du\)와 \(\Delta \mathbf x_2=\mathbf x_v dv\)를 두 변으로 하는 평행사변형의 넓이로 근사된다.
(Note) 위 근사는 \(du, dv\)에 대한 \(\Delta R\)의 넓이의 일차 근사식이고, 평행사변형의 두 변은 \(d\mathbf x=\mathbf x_u du+\mathbf x_v dv\)로부터 비롯된 것이다.

두 벡터 \(\mathbf v_1, \mathbf v_2\)를 이웃한 두 변으로 하는 평행사변형의 넓이는 \(|\mathbf v_1\times \mathbf v_2|\)이므로 \(\Delta R\)의 넓이를 \(\Delta s\)라 하면 \[\Delta s=|\Delta \mathbf x_1\times \Delta \mathbf x_2|=|\mathbf x_u\times \mathbf x_v|\,dudv=\sqrt{EG-F^2\, }dudv\]이다. 따라서 다음과 같이 곡면 위의 영역 \(R\)의 넓이를 다음과 같이 정의한다.
[Definition 9.5]
곡면의 \(C^1\)급 이상인 매개변수 평면 위의 열린 집합 \(W\)에서 정의된 좌표 조각 \(\mathbf x=\mathbf x(u, v)\)에 대하여 이 좌표 조각의 상이 포함하는 영역 \(R\)의 넓이는 \[A=\iint_W \sqrt{EG-F^2\,}dudv\]
[Example 9.6]
유향 곡면의 경우 위와 같이 정의된 곡면의 넓이는 매개변수의 종류의 영향을 받지 않는다. \(\mathbf x=\mathbf x^*(\theta, \phi)\)를 곡면 위의 영역 \(R\)을 포함하고, 각 \((u, v)\in W\)에 대하여 \(\partial(\theta, \phi)/\partial(u, v)>0\)을 만족시키는 적당한 좌표 조각이라고 하자. 그러면 계산을 통해 \[EG-F^2=\left(E^*G^*-F^{*2}\right)[\partial(\theta, \phi)/\partial(u, v)]^2\]임을 알 수 있다. 그러면 이중적분의 변환에 따라 \[\begin{align}A&=\iint_W \sqrt{EG-F^2}\,dudv\\[.4em]&=\iint_W\sqrt{E^*G^*-F^{*2}}\, \frac{\partial(\theta, \phi)}{\partial(u, v)}\,dudv\\[.4em]&=\iint_{W^*}\sqrt{E^*G^*-F^{*2}}\,d\theta d\phi=A^* \end{align}\]임을 알 수 있다.
[Example 9.7]
\(z\)축 둘레로의 토러스 \[\mathbf x=((b+a\sin\phi)(\cos\theta), \ (b+a\sin\phi)(\sin\theta), \ a\cos\phi)\]에 대하여 계산을 통해 \[E=\mathbf x_\theta\cdot \mathbf x_\theta=(b+a\sin\phi)^2, \ \ F=\mathbf x_\theta\cdot \mathbf x_\phi=0, \ \ G=\mathbf x_\phi \cdot \mathbf x_\phi=a^2\]를 얻는다. 따라서 토러스의 겉넓이는 \[\begin{align}S&=\iint_W\sqrt{EG-F^2}\, d\theta d\phi\\[.4em]&=\int_0^{2\pi}\left[\int_0^{2\pi} a(b+a\sin\phi)d\phi\right] d\theta=4\pi^2ab\end{align}\]
제2기본형식
제1기본형식은 앞에서 본 것과 같이 곡면의 접벡터를 이용하여 정의되는 개념이다. 이에 반해 제2기본형식은 곡면의 법벡터를 이용하여 정의되는 개념이다. 곡면 위의 \(C^2\)급 이상인 좌표 조각 \(\mathbf x=\mathbf x=(u, v)\)에 대하여 점 \(\mathbf x(u, v)\)에서의 단위 법선 벡터 \(\mathbf N\)은 \(\mathbf N=\displaystyle \frac{\mathbf x_u\times \mathbf x_v}{|\mathbf x_u\times \mathbf x_v|}\)으로 주어진다. 이때 미분 \(d\mathbf N=\mathbf N_u du+\mathbf N_v dv\)에 대하여 \[\mathbf N\cdot \mathbf N=1 \ \Rightarrow \ \mathbf N\cdot d\mathbf N=0\]이므로 \(d\mathbf N\)은 그 점에서의 접평면에 평행한 벡터이다.

이때 다음과 같은 \(du, dv\)에 관한 함수 \[\begin{align}\mathrm {II}&=-d\mathbf x\cdot d\mathbf N=-(\mathbf x_udu+\mathbf x_vdv)\cdot(\mathbf x_udu+\mathbf x_vdv)\\[.4em] &=-(\mathbf x_u\cdot \mathbf N_u)du^2-(\mathbf x_u\cdot \mathbf N_v+\mathbf x_v\cdot \mathbf N_u)dudv-(\mathbf x_v\cdot \mathbf N_v)dv^2\\[.4em]&=Ldu^2+2Mdudv+Ndv^2 \\[.4em] &\quad (L=-\mathbf x_u\cdot \mathbf N_u, \; M=-\frac{1}{2}(\mathbf x_u\cdot \mathbf N_v+\mathbf x_v\cdot \mathbf N_u), \; N=-\mathbf x_v\cdot \mathbf N_v)\end{align}\]를 \(\mathbf x=\mathbf x(u, v)\)의 제2기본형식이라고 한다.
[Definition 9.8]
곡면 위의 \(C^2\)급 이상인 좌표 조각 \(\mathbf x=\mathbf x=(u, v)\)에 대하여 \[\begin{align}&\mathrm {II}(du, dv)=Ldu^2+2Mdudv+Ndv^2 \\[.4em] & (L=-\mathbf x_u\cdot \mathbf N_u, \; M=-\frac{1}{2}(\mathbf x_u\cdot \mathbf N_v+\mathbf x_v\cdot \mathbf N_u), \; N=-\mathbf x_v\cdot \mathbf N_v)\end{align}\]을 점 \(\mathbf x(u, v)\)에서의 제2기본형식(the second fundamental form)이라 하고, 위의 \(L, \, M, \, N\)을 제2기본계수(the second fundamental coefficient)라고 한다.
제1기본형식과 비슷하게 제2기본형식 또한 매개변수 변환에 의하여 값이 변하지 않는다. 다른 좌표 조각 \(\mathbf x=\mathbf x^*(\theta, \phi)\)에 대하여 두 좌표 조각 \(\mathbf x=\mathbf x(u, v)\)와 \(\mathbf x=\mathbf x^*(\theta, \phi)\)에 대하여 두 좌표 조각의 공통 부분에서 야코비 행렬식의 값이 양수(유향 곡면)이면 \[\begin{align}&L=L^*\theta_u^{\,2}+2M^*\theta_u\phi_u+N^*\phi_u^{\,2}\\[.4em]&M=L^*\theta_u\theta_v+M^*(\phi_u\theta_v+\theta_u\phi_v)+N^*\phi_u\phi_v\\[.4em] &N=N^*\theta_v^{\, 2}+2M^*\theta_v\phi_v+N^*\phi_v^{\, 2}\end{align}\]임을 이용하여 이차형식의 값이 동일함을 어렵지 않게 증명할 수 있다.
한편, \(\mathbf x_u\)와 \(\mathbf x_v\)는 \(\mathbf N\)과 각각 수직이므로 각 \((u, v)\)에 대하여 \(\mathbf x_u\cdot \mathbf N=\mathbf x_v\cdot \mathbf N=0\)이다. 이 등식들의 양변을 미분하면
\[\begin{align}&\mathbf x_u\cdot \mathbf N=0 \ \Rightarrow \ \mathbf x_{uu}\cdot \mathbf N+\mathbf x_u\cdot \mathbf N_u=0, \\[.4em] &\mathbf x_u\cdot \mathbf N=0\ \Rightarrow \ \mathbf x_{uv}\cdot \mathbf N+\mathbf x_u\cdot \mathbf N_v=0, \\[.4em]&\mathbf x_v\cdot \mathbf N=0 \ \Rightarrow \ \mathbf x_{vu}\cdot \mathbf N+\mathbf x_v\cdot \mathbf N_u=0, \\[.4em] &\mathbf x_v\cdot \mathbf N=0 \ \Rightarrow \ \mathbf x_{vv}\cdot \mathbf N+\mathbf x_v\cdot \mathbf N_v=0 \end{align}\]을 얻는다. 또한 \(\mathbf x=\mathbf x(u, v)\)는 \(C^2\)급 이상이므로 \(\mathbf x_{uv}=\mathbf x_{vu}\)이다. 이로부터 다음과 같이 제2기본계수를 계산할 수 있다.
[Theorem 9.9]
좌표조각 \(\mathbf x=\mathbf x(u, v)\)의 제2기본계수 \(L, \, M, \, N\)은 \[L=\mathbf x_{uu}\cdot \mathbf N, \ \ M=\mathbf x_{uv}\cdot \mathbf N, \ \ N=\mathbf x_{vv}\cdot \mathbf N\]
[Example 9.10]
곡면 \(\mathbf x=(u,\, v, \,u^2-v^2)\)에 대하여 \[\begin{align}&\mathbf x_u=(1,\, 0, \,2u), \; \mathbf x_v=(0,\, 1, \, -2v)\\[.5em] & \Rightarrow \ \mathbf N=\frac{\mathbf x_u\times \mathbf x_v}{|\mathbf x_u\times\mathbf x_v|}=\frac{1}{\sqrt{1+4(u^2+v^2)}}\,(-2u, \, -2v, \, 1)\end{align}\]이고, \[\begin{align}&\mathbf x_{uu}=(0, 0, 2), \; \mathbf x_{uv}=(0, 0, 0), \; \mathbf x_{vv}=(0, 0, -2) \\[.5em]&\Rightarrow \ L=\mathbf x_{uu}\cdot \mathbf N=\frac{2}{\sqrt{1+4(u^2+v^2)}}, \\[.5em] &\quad \ \ M=\mathbf x_{uv}\cdot \mathbf N=0, \\[.4em] &\quad \ \ N=\mathbf x_{vv}\cdot \mathbf N=-\frac{2}{\sqrt{1+4(u^2+v^2)}}\end{align}\]이므로 \[\mathrm {II}=Ldu^2+2Mdudv+Ndv^2=\frac{2(du^2-dv^2)}{\sqrt{1+4(u^2+v^2)}}\]이다.
제2기본형식의 가장 중요한 기능 중 하나는 곡면의 국소적인 모양을 결정한다는 것이다. 그림과 같이 곡면의 한 점 \(\rm P\)과 그 근방의 한 점 \(\rm Q\)를 포함하는 곡면의 좌표 조각 \(\mathbf x=\mathbf x(u, v)\)에 대하여 \(d=\vec{\mathrm {PQ}} \cdot \mathbf N\)을 벡터 \(\rm PQ\)의 단위 법벡터 \(\mathbf N\) 위로의 사영이라 하자.

점 \(\rm P\)의 위치 벡터를 \(\mathbf x(u, v)\)라 하고, 점 \(\rm Q\)의 위치 벡터를 \(\mathbf x(u+du, \, v+dv)\)라 하면 벡터함수의 테일러 정리에 의하여 \[\mathbf x(u+du, \, v+dv)=\mathbf x(u, v)+d\mathbf x+\frac{1}{2}d^2\mathbf x+\mathbf o(du^2+dv^2)\]이므로 \[\begin{align}d&=\vec {\mathrm {PQ}}\cdot \mathbf N=(\mathbf x(u+du, \, v+dv)-\mathbf x(u, v))\cdot \mathbf N\\[.5em] &=\left[d\mathbf x+\frac{1}{2}d^2\mathbf x+\mathbf o(du^2+dv^2)\right]\cdot \mathbf N\\[.3em]&=d\mathbf x\cdot \mathbf N+\frac{1}{2}d^2\mathbf x\cdot \mathbf N+\mathbf o(du^2+dv^2)\\[.4em]&=\frac{1}{2}d^2\mathbf x\cdot \mathbf N+o(du^2+dv^2)\quad (\because d\mathbf x\cdot \mathbf N=0)\\[.4em]&=\frac{1}{2}\mathrm {II}+\mathbf o(du^2+dv^2)\end{align}\]이다. 따라서 곡면의 제2기본형식 \(\rm {II}\)의 크기인 \(\rm |II|\)는 근사적으로 점 \(\rm Q\)에서 점 \(\rm P\)에서의 접평면으로 내린 수선의 길이와 같다. 이를 이용하여 \(d=0\)이 되는 방향 \((du, dv)\)의 개수에 따라 다음과 같은 세 가지 경우로 나눌 수 있다.
(1) 타원점(Elliptic point): 점 \(\rm P\)에서 \(LN-M^2>0\)인 경우 \(II=0\)이 되는 방향 \((du, \, dv)\)가 존재하지 않는다. (이차방정식의 판별식을 생각하면 된다.) 이 경우 \(\rm P\)의 근방에서 \(d=0\)인 \((du, \, dv)\)가 존재하지 않는다. \(\rm II\)는 \(du, dv\)에 대한 \(C^2\)급 이상의 함수이므로 \(\rm P\)의 근방에서 \(d\)의 부호가 일정하다. 즉, \(\rm P\)에서의 접평면을 기준으로 곡면은 그림과 같이 한 쪽에만 위치하게 된다.
(2) 쌍곡점(Hyperbolic point): 점 \(\rm P\)에서 \(LN-M^2<0\)인 경우 \(II=0\)이 되는 방향 \((du, \, dv)\)가 두 가지 존재한다. 즉, 이 경우 점 \(\rm P\)를 지나면서 \(d=0\)인 곡선이 접평면 위에 2개 존재하게 된다. 이 2개의 곡선을 기준으로 나누어진 4개의 영역에서 \(d\)의 부호가 양과 음을 모두 취하게 되고, 곡면은 접평면을 기준으로 양쪽에 다 놓이게 된다.
(3) 포물점(Parabolic point): 점 \(\rm P\)에서 \(LN-M^2=0\)이고 \(L^2+M^2+N^2\neq 0\)인 경우(즉, \(L, \, M, \, N\) 중 적어도 하나는 \(0\)이 아닌 경우), \(II=0\)이 되는 방향 \((du, \, dv)\)가 단 하나 존재한다. 즉, 이 경우 \(\rm P\)를 지나며 \(d=0\)이 되는 곡선이 접평면 위에 단 하나 존재한다. 이러한 점이 아닌 경우에는 \(d\)의 부호가 일정하며, 접평면을 기준으로 곡면이 한쪽에만 위치한다.
(4) 평면점(Planar point): 점 \(\rm P\)에서 \(L=M=N=0\)인 경우, 모든 방향 \((du, \, dv)\)에 대해서 \(d=0\)이다. 즉, 그 점에서는 접평면에 근사한다. (이 경우에는 접촉면(contact)의 차수가 이전의 경우보다 높은 경우이다.)

[Example 9.11]
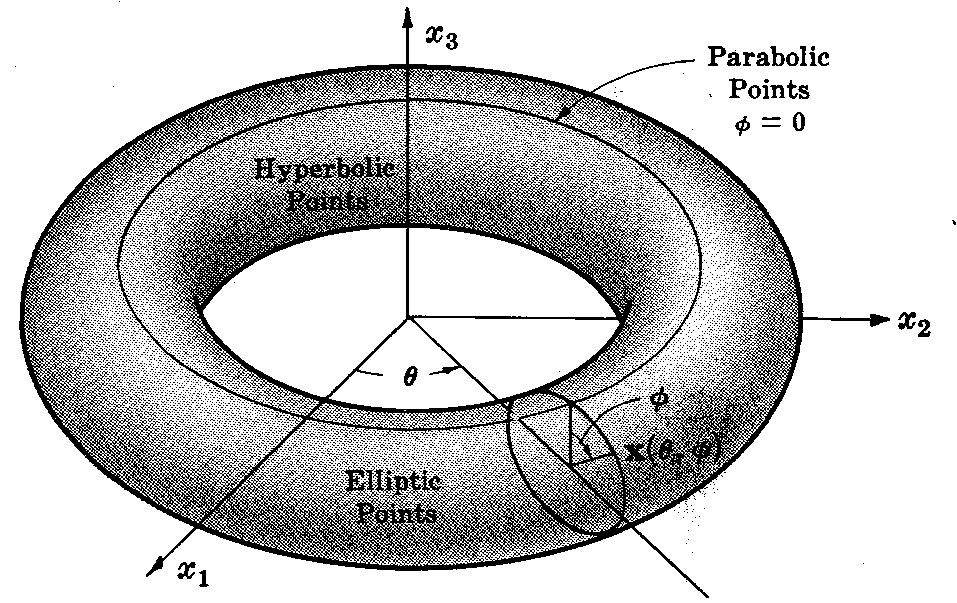
토러스 \[\mathbf x=((b+a\sin\phi)(\cos\theta), \ (b+a\sin\phi)(\sin\theta), \ a\cos\phi) \; (b>a)\]에 대하여 계산을 통해 \[\begin{align}& \mathbf x_{\theta\theta}=(-(b+a\sin\phi)(\cos\theta), \, -(b+a\sin\phi)(\sin\theta), \ 0), \\[.5em]&\mathbf x_{\theta\phi}=(-a\cos\phi\sin\theta, \ a\cos\phi\cos\theta, \ 0),\\[.5em] &\mathbf x_{\phi\phi}=(-a\sin\phi\cos\theta, \, -a\sin\phi\sin\theta, \, -a\cos\phi), \\[.5em] &\mathbf N=(-\cos\theta\sin\phi, \, -\sin\theta\sin\phi, \, -\cos\phi) \end{align}\]이므로 \[L=\mathbf x_{\theta\theta} \cdot \mathbf N=(b+a\sin\phi)\sin\phi, \ \ M=\mathbf x_{\theta\phi}\cdot \mathbf N=0, \ \ N=\mathbf x_{\phi\phi}\cdot \mathbf N=a\]
이다. 따라서 \(LN-M^2=a(b+a\sin\phi)\sin\phi\)이다.
\(b>a\)에서 \(b+a\sin\phi>0\)이다. 따라서 \(LN-M^2\)의 부호는 \(\sin\phi\)의 부호에 따라 결정된다. 따라서 매개변수 곡선 \(\phi=0, \; \phi=\phi\) 위의 점들은 (즉, 토러스에서 \(z\)의 절댓값이 가장 큰 점들의 집합) 모두 포물점이고, \(0<\theta<\phi\)의 영역의 점들은 (즉, 토러스의 바깥 면) 타원점이고, \(\phi<\theta<2\phi\)인 점들은 (즉, 토러스의 안쪽 면) 모두 쌍곡점이다.
Reference: <Schaum's Outlines: Differential Geometry> Martin Lipschultz, 1969
'[Undergraduates] > 미분기하학' 카테고리의 다른 글
| [Chapter 9] First and Second Fundamental Forms - (2) (0) | 2021.07.17 |
|---|---|
| [Chapter 8] Concept of a Surface - (2) (0) | 2021.05.24 |
| [Chapter 8] Concept of a Surface - (1) (0) | 2021.05.12 |