(Note) 이 문서는 교재의 연습 문제 중에서 다른 문제를 해결할 때 유용할 법한 명제들을 정리한 것입니다. 앞으로도 내용이 추가될 수 있습니다.
<Chapter 1: Sets and Relations>
[Theorem 1.0]
세 집합 \(A, \, B, \, C\)에 대하여 \(A\times (B\cap C)=(A\times B)\cap (A\times C)\)이고 \(A\times (B\cup C)=(A\times B)\cup (A\times C)\)이다.
# 증명 ▶
(Proof)
\[\begin{align}A\times (B\cap C)&=\{(a, b)\,|\, a\in A, \ b\in B\cap C\}\\[.4em]&=\{(a, b) \, |\, a\in A, \ b\in B\}\cap \{(a, b)\, |\, a\in A, \ b\in C\}\\[.4em]&=(A\times B)\cap (A\times C)\end{align}\] 비슷한 방법으로 \(A\times (B\cup C)=(A\times B)\cup (A\times C)\)도 보일 수 있다.
# ◀ 닫기
[Theorem 1.1]
두 집합 \(A, \, B\)에 대하여 \(2^A\)와 \(2^B\)를 각각 \(A, \, B\)의 멱집합(power set)이라 하자. 그러면 다음이 성립한다.
\[\text{(i) }\ 2^A\cap 2^B=2^{A\cap B}, \quad \text{(ii) }\ 2^A\cup 2^B\subset 2^{A\cup B}\]
# 증명 ▶
(Proof)
\[\begin{align}\text{(i):}\ \ 2^A\cap 2^B&=\{G\, |\, G\in2^A, \ G\in 2^B\}\\[.4em]&=\{G\, |\, G\subset A, \ G\subset B\}\\[.4em]&=\{G\, |\, G\subset A\cap B\}=2^{A\cap B}\end{align}\]\[\begin{align}\text{(ii):}\ \ 2^A\cup 2^B&=\{G\, |\, G\in2^A \ \text{ or } \ G\in 2^B\}\\[.4em]&=\{G\, |\, G\subset A\ \text{ or }\ G\subset B\}\\[.4em]&\color{red}\subset\color{black}\{G\, |\, G\subset A\cup B\}=2^{A\cup B}\end{align}\] (Note) \(\text{(ii)}\)에서 \(G\subset A\) 또는 \(G\subset B\)이면 \(A,\, B\subset A\cup B\)이므로 \(G\subset A\cup B\)가 성립한다. 그러나 \(G\subset A\cup B\)라고 해서 \(G\subset A\)이거나 \(G\subset B\)인 것은 아니다. 예를 들어 \(A=\{1, 2\}, \ B=\{3, 4\}\)인 경우 \(G=\{1, 3\}\)이라 하면 \(G\not\subset A\)이고 \(G\not\subset b\)이지만 \(G\subset A\cup B\)이다.
# ◀ 닫기
<Chapter 2: Functions>
[Theorem 2.0]
두 함수 \(f: A\to B\)와 \(g: B\to A\)가 \[g\circ f=1_A, \ \ f\circ g=1_B\]를 만족시키면, \(f^{-1}:B\to A\)가 존재하고 \(g=f^{-1}\)이다. (단, \(1_A: A\to A\)와 \(1_B: B\to B\)는 항등함수이다.)
# 증명 ▶
(Proof)
두 함수 \(f, \, g\)가 일대일대응임을 보이면 충분하다. \(g\circ f=1_A\)이므로 \(x_1, \, x_2\in A\)에 대하여 \[f(x_1)=f(x_2) \ \Rightarrow \ g(f(x_1))=g(f(x_2)) \ \Rightarrow \ x_1=x_2\]이므로 \(f\)는 일대일이다. 또한 임의의 \(y_0\in B\)에 대하여 \((f(g(y_0))=y_0\)가 성립하므로 \(f\)는 전사(surjective)이다. 따라서 \(f\)는 \(A\)에서 \(B\)로의 일대일대응이다. 비슷한 방법으로 \(g\) 또한 일대일대응임을 보일 수 있다.
# ◀ 닫기
[Theorem 2.1]
\(f: X\to Y\)와 임의의 \(A, \, B\subset X\)에 대하여 다음이 성립한다. \[\begin{align}&\text{(i) }f[A\cup B]=f[A]\cup f[B], \qquad \text{(ii) }f[A\cap B]\subset f[A]\cap f[B]\\[.4em]&\text{(iii) } f[A-B]\supset f[A]-f[B], \quad \ \text{(iv) }A\subset B\ \Rightarrow \ f[A]\subset f[B]\end{align}\] (Note) 교집합 연산이 들어가는 경우에는 등호가 성립하지 않는다고 기억해두면 된다.
# 증명 ▶
(Proof)
(ii)의 경우만 증명하도록 한다. 나머지도 비슷한 방법으로 증명할 수 있다. \[\begin{align}y\in f(A\cap B) &\Rightarrow \exists\, x\in A\cap B : f(x)=y\\[.4em]&\Rightarrow \exists\, (x\in A \, \wedge \, x\in B): f(x)=y\\[.4em]&\Rightarrow y\in f[A]\wedge y\in f[B]\\[.4em]&\Rightarrow y\in f[A]\cap f[B] \end{align}\] (Cf) (ii), (iv)에서 등호가 성립하지 않는 예로 다음을 들 수 있다. 함수 \(\pi: \Bbb R^2\to \Bbb R\)을 \(\pi(x, y)=x\)라 정의하고 \(\Bbb R^2\)의 두 부분집합 \(A, \, B\)를 \(A=[1, 2]\times [1, 2], \; B=[1, 2]\times [3, 4]\)라 두면 (ii), (iii)에서 반대쪽 방향의 포함 관계는 성립하지 않음을 쉽게 알 수 있다.
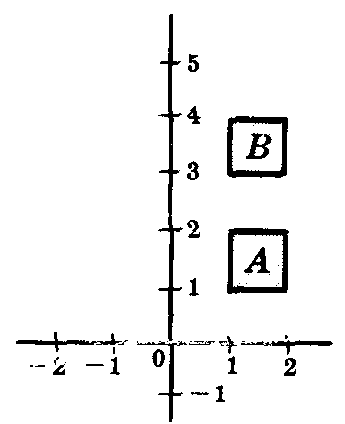
# ◀ 닫기
[Theorem 2.2]
\(f: X\to Y\)와 임의의 \(A, \, B\subset Y\)에 대해 다음이 성립한다. \[\begin{align}&\text{(i) }f^{-1}[A\cup B]=f^{-1}[A]\cup f^{-1}[B], \qquad \text{(ii) }f^{-1}[A\cap B]= f^{-1}[A]\cap f^{-1}[B]\\[.4em]&\text{(iii) } f^{-1}[A-B]= f^{-1}[A]-f^{-1}[B], \quad \, \text{(iv) }A\subset B\ \Rightarrow \ f^{-1}[A]\subset f^{-1}[B]\end{align}\] (Note) 역사상의 집합 연산은 단순히 매우 잘 작동한다(well-behaved)고 생각하면 된다.
# 증명 ▶
(Proof)
(ii)의 경우만 증명하도록 한다. 나머지도 비슷한 방법으로 증명할 수 있다. \[\begin{align}(\subset)\; x\in f^{-1}(A\cap B) &\Rightarrow f(x)\in A\cap B\\[.4em]&\Rightarrow f(x)\in A\wedge f(x)\in B\\[.4em]&\Rightarrow x\in f^{-1}[A]\wedge x\in f^{-1}[B]\\[.4em]&\Rightarrow x\in f^{-1}[A]\cap f^{-1}[B] \end{align}\] \[\begin{align}(\supset)\; x\in f^{-1}(A)\cap f^{-1}[B] &\Rightarrow x\in f^{-1}[A]\wedge x\in f^{-1}[B]\\[.4em] & \Rightarrow f(x)\in A\wedge f(x)\in B \\[.4em]&\Rightarrow f(x)\in A\cap B \\[.4em]&\Rightarrow x\in f^{-1}(A\cap B) \end{align}\] (Note) (iii)을 이용하면 \(f^{-1}[A^c]=(f^{-1}[A])^c\)가 성립함을 알 수 있다.
# ◀ 닫기
[Theorem 2.3]
함수 \(f: X\to Y\)에 대하여 \(A\subset X\), \(B\subset Y\)라 하자. 그러면 다음이 성립한다. \[\text{(i) } A\subset f^{-1}\circ f[A] \qquad \text{(ii) } B\supset f\circ f^{-1}[B]\]
# 증명 ▶
(Proof)
어렵지 않으므로 직접 해보면 된다. [Theorem 2.2]에서의 방법을 그대로 적용하면 된다.
(Note) \(A=f^{-1}\circ f[A]\)일 필요충분조건은 \(f\)가 일대일인 것이고, \(B=f\circ f^{-1}[B]\)일 필요충분조건은 \(f\)가 전사인 것이다. 예를 들어 \(f\)가 일대일인 경우, \[\begin{align} x\in f^{-1}\circ f[A] &\Rightarrow f(x)\in f[A]\\[.4em]&\Rightarrow f(x)\in \{y:y=f(x) \ \text{for some }x\in A\}\\[.4em]&\Rightarrow x\in A \; (\because \ f:1-1)\\ \end{align}\]이다. 마찬가지로 \(f\)가 전사인 경우 \[\begin{align} y\in B &\Rightarrow \exists\, x\in f^{-1}[B]: f(x)=y \ \ (\because f:\text{onto})\\[.4em]&\Rightarrow y=f(x)\in f\circ f^{-1}[B]\\[.4em] \end{align}\]가 성립한다.
# ◀ 닫기
[Theorem 2.4]
\(A\)를 임의의 집합이라 하고, 각 \(p\in A\)에 대하여 집합 \(G_p\)를 \(A\)의 부분집합 중에서 \(p\in G_p\subset A\)를 만족시키는 것이라 하자. 그러면 \(A=\bigcup \{G_p: p\in A\}\)임을 보여라.\
(Note) 이는 위상수학에서 열린 집합을 표현할 때 쓰이는 방법이다.
# 증명 ▶
(Proof)
\(B=\bigcup \{G_p: p\in A\}\)라 하자. 그러면 \(B\)는 \(A\)의 각 원소를 포함하므로 \(A\subset B\)이다. 역으로, \(x\in B\)라 하면 대하여 적당한 \(p_0\in A\)가 존재하여 \(x\in G_{p_0}\subset A\)를 만족시킨다. 따라서 \(x\in A\)이다. 이로부터 \(A=B\)를 얻는다.
# ◀ 닫기
[Theorem 2.5]
\(A\)를 집합 \(U\)의 임의의 부분집합이라고 하자. 다음과 같이 정의된 함수 \(\chi_A: U\to \Bbb R\) \[\chi_A(x)=\begin{cases}1 & (x\in A)\\[.4em]0 & (x\notin A)\end{cases}\]를 \(A\)의 특성함수(characteristic function)라고 한다. 이때 다음이 성립함을 보여라. \[\text{(i) }\chi_{A\cap B}=\chi_A\chi_B \quad \text{(ii) }\chi_{A\cup B}=\chi_A+\chi_B-\chi_{A\cap B} \quad \text{(iii) }\chi_{A-B}=\chi_A-\chi_{A\cap B}\]
# 증명 ▶
(Proof)
\(\text{(i):}\) \(\chi_{A\cap B}(x)=1\)일 필요충분조건은 \(x\in A\cap B\)인 것이다. 즉, \(x\in A\)이고 \(x\in B\)인 것이다. 따라서 \(\chi_{A\cap B}(x)=1 \ \Leftrightarrow \ \chi_A\chi_B(x)=1\)이다. \(\chi\)는 함숫값이 \(0\) 또는 \(1\)뿐이므로 \(\chi_{A\cap B}=\chi_A\chi_B\)가 성립한다.
(ii), (iii)은 경우를 나누어서 (즉, \(x\)가 \(A\) 또는 \(B\)의 원소인지에 따라 경우를 분류하여) 위와 같은 방법으로 직접 확인해보면 된다.
# ◀ 닫기
<Chapter 3: Cardinality, Order>
[Theorem 3.0]
모든 무한집합은 가부번집합을 부분집합으로 가진다.
# 증명 ▶
(Proof)
집합 \(A\)가 무한집합이라고 하자. 임의의 \(a_1\in A\)를 택하여 집합 \(A-\{a_1\}\)을 생각하면, 이는 여전히 무한집합이다. 그렇지 않다면, \(A\) 또한 유한집합이어야 한다. 비슷한 방법으로 \(a_2\in A-\{a_1\}\)을 택하여 집합 \(A-\{a_1, \, a_2\}\)를 생각하면 이 집합 또한 무한집합이다. 이런 식으로 모든 자연수 \(n\)에 대하여 \(A-\{a_1, \, a_2, \, \cdots, \, a_n\}\)은 무한집합이므로 이런 식으로 구성된 원소들의 집합 \(\{a_1, \, a_2, \, \cdots, \}\)은 \(A\)의 가부번집합이다.
# ◀ 닫기
[Theorem 3.1]
집합족 \(\{A_n: n\in \Bbb N\}\)을 가산집합(countable)들의 가산집합족(countable class)이라고 하자. 그러면 \(\bigcup_{n\in \Bbb N} A_n\)은 가산집합이다. (간략하게 말하면, 가산집합의 가산 합집합은 가산집합이다.)
# 증명 ▶
(Proof)
자연수 \(n\)에 대하여 집합 \(A_n\)을 다음과 같이 표현하자. \[\begin{align}&A_1=\{a_{11}, \, a_{12}, \, \cdots, \, a_{1n},\, \cdots\}\\[.4em]&A_2=\{a_{21}, \, a_{22}, \, \cdots, \, a_{2n},\, \cdots\}\\[.3em]&\qquad \qquad\qquad \cdots\\[.4em] &A_n=\{a_{n1}, \, a_{n2}, \, \cdots, \, a_{nn},\, \cdots\}\\[.4em]& \qquad \qquad \qquad \cdots \end{align}\] 그러면 자명히 \(\bigcup_{n\in \Bbb N}A_n\)은 \(\Bbb N\times \Bbb N\)의 부분집합과 대등하다. 따라서 \(\Bbb N\times \Bbb N\)이 가산집합임을 보이면 충분하다.
함수 \(f: \Bbb N\times \Bbb N\to \Bbb N\)을 \(f(m,\, n)=2^m\cdot 3^n\)으로 정의하자. 그러면 소인수분해의 유일성에 의하여 함수 \(f\)는 일대일함수이다. 따라서 \(\Bbb N\times \Bbb N\)은 \(\Bbb N\)의 부분집합과 대등하다. 따라서 \(\Bbb N\times \Bbb N\)은 가산집합이다.
# ◀ 닫기
[Theorem 3.2] (Schroeder-Bernstein)
\(X\supset Y\supset X_1\)이고 \(X\sim X_1\)이면 \(X\sim Y\)이다.
(Note1) \(X\sim Y\)는 \(X\)에서 \(Y\)로의 일대일대응이 존재함을 의미한다.
(Note2) 위 정리는 다음과 동치이다: 두 집합 \(X, \, Y\)에 대하여 \(X\)에서 \(Y\)로의 일대일함수가 존재하고, \(Y\)에서 \(X\)로의 일대일함수가 존재하면 \(X\)에서 \(Y\)로의 일대일대응이 존재한다.
# 증명 ▶
(Proof)
다음 글의 [Theorem 3.6]을 참조하면 된다:
무한(infinite)이란 무엇인가?
집합의 크기 집합의 원소가 유한인 경우, 직접 세어서 어떤 것이 더 많은지 알 수 있으나 원소의 개수가 유한하지 않은 경우 직관적으로 어떤 집합이 더 '큰' 집합인지 알기 어렵다. 집합론에서
greenland.tistory.com
# ◀ 닫기
[Theorem 3.3] (조른의 보조정리: Zorn's Lemma)
\(X\)가 부분순서집합(partially ordered set)이라 하고, \(X\)의 모든 전순서 부분집합(totally ordered subset)이 상계(upper bound)를 가진다고 하자. (즉, 위로 유계라고 하자.) 그러면 \(X\)는 적어도 하나의 극대 원소를 가진다.
(Note) 조른의 보조 정리는 선택 공리(The Axiom of Choice)와 정렬 원리(Well-ordering Principle)와 동치이다.
# 증명 ▶
(Proof)
증명은 보통 선택 공리를 이용하여 '서수(ordinal number)'라는 개념을 이용한다. 이는 수준이 학부의 일반위상수학의 범위를 넘어서므로 생략한다.
# ◀ 닫기
Reference: <SCHAUM'S outlines: General Topology>, Seymour Lipschutz.
'[Undergraduates] > 위상수학' 카테고리의 다른 글
| [Chapter 13] 연결성 - (2) (2) | 2021.06.09 |
|---|---|
| [Chapter 13] 연결성 - (1) (0) | 2021.05.25 |
| [Chapter 12] 곱공간 (0) | 2021.05.09 |